Viscosity

The story of viscosity is quite fascinating and dates back to ancient civilizations, but it was not until the 19th century that significant strides were made in understanding this fluid property scientifically.

The term “viscosity” comes from the Latin word “viscum,” which refers to the sticky sap of the mistletoe plant. This sap was used as a glue in traps to catch birds. This gives us an early indication of humanity’s interest in the properties of sticky, resistant substances.

Newton was the first to conceptualize and quantify the idea of viscosity. He proposed that for simple fluids, the rate at which they flow (or their resistance to flowing) is directly proportional to the force applied to them. This relationship is now known as Newton’s law of viscosity.

Poiseuille, a French physician, is known for his work on blood flow and viscosity. He conducted experiments to measure the flow of blood through capillary tubes and formulated Poiseuille’s law, which describes the flow rate of a fluid through a pipe.

The modern scientific study of viscosity began with the work of Jean Léonard Marie Poiseuille, a French physicist. Born in Paris in 1799, Poiseuille initially studied medicine but later shifted his focus to physics. His interest in blood flow led him to investigate the resistance of fluids to flow through narrow tubes.

In 1829, Poiseuille set up experiments to test the flow of liquids through tubes of different sizes. He discovered that the flow rate of a liquid is determined by its viscosity, as long as the pressure gradient, length, and diameter of the tube are constant. Through his experiments, he found that factors like tube pressure, temperature, diameter, and length all affected a fluid’s viscosity.

Poiseuille’s most notable contribution was the development of an equation, now known as Poiseuille’s Law, which allows the calculation of viscosity based on these factors. This law became a fundamental principle in fluid dynamics and is still used today to determine the viscosity of various substances, from human blood to molten lava.

Hagen, along with Poiseuille, independently discovered the law governing laminar flow in cylindrical pipes. This law is sometimes referred to as the Hagen-Poiseuille law.

In honor of his contributions, the unit of viscosity in the metric system is named the poise (or poiseuille). This unit measures the thickness or resistance to flow of a liquid, with water having a lower viscosity compared to thicker liquids like honey or oil.

What is Viscosity?

Viscosity is essentially a fluid’s resistance to flow. It describes how thick or thin a fluid is. Imagine you’re trying to push a book across your desk. If the desk is smooth, the book slides easily. But if there’s a sticky substance on the desk, like honey, it’s much harder to push the book. This resistance you feel is similar to what we call viscosity in fluids.

Viscosity is a measure of a fluid’s resistance to flow. It describes how “thick” or “sticky” a fluid is, and how much it resists being deformed or moved. Here’s a simple way to think about it:

• Water is “thin,” so it has a low viscosity; it flows easily.
• Honey is “thick,” so it has a high viscosity; it flows slowly.

In more scientific terms, viscosity is the internal friction between layers of a fluid that are moving at different speeds. When you pour water, the layers slide over each other easily, but with honey, the layers don’t want to move as much; they stick together, and that’s why it pours slowly.

So, when we define viscosity, we’re talking about this internal friction or resistance to flow. If you’re trying to visualize it, think about swimming in a pool versus swimming in a pool filled with honey. In which scenario would it be harder to move? The honey pool, right? That’s because of its higher viscosity.

\(\displaystyle \eta = \frac{\text{shear stress}}{\text{rate of shear strain}} \)

\(\displaystyle\eta = \frac{F}{A \cdot \frac{dv}{dx}} \)

Here, (η) is the viscosity, (F) is the force applied, (A) is the area, (dv) is the change in velocity, and (dx) is the change in distance.

• Shear stress is the force per unit area applied parallel to the fluid’s surface.
• The rate of shear strain is the change in velocity with respect to the distance between the fluid layers.

The viscosity formula is all about understanding the relationship between the force applied to a fluid and how it moves.
Imagine you have a stack of paper, and you push the top sheet. The force you apply causes the sheets to slide over each other. The same happens in fluids; the layers slide over each other, and viscosity measures how much force is needed to do this at a certain rate.

Units of Viscosity:
Viscosity is measured in pascal-seconds (Pa·s) in the SI system. But you might also hear about the poise (P), which is used in the CGS system. To give you an idea, water at room temperature has a viscosity of about 0.001 Pa·s or 1 centipoise.

Dimensional Formula of Viscosity:
The dimensional formula is like a recipe that tells us what physical quantities are needed to express viscosity. For viscosity, the dimensional formula is:

\(\displaystyle [M^1L^{-1}T^{-1}] \)

So, viscosity is expressed in terms of one unit of mass, one unit of length taken in the negative sense (because it’s in the denominator), and one unit of time also in the negative sense. In simpler terms, this formula tells us how much force is needed to move one layer of fluid over another layer at a certain speed and distance apart.

Types of Viscosity

Viscosity is a fundamental property of fluids that characterizes their resistance to flow. It plays a crucial role in various fields, including engineering, physics, chemistry, and biology. Understanding viscosity is essential for predicting fluid behavior, designing efficient systems, and optimizing processes in numerous applications. Two main types of viscosity, dynamic viscosity, and kinematic viscosity, provide valuable insights into how fluids behave under different conditions.

Dynamic Viscosity (Absolute Viscosity):

Dynamic viscosity (absolute viscosity) measures the fluid’s resistance to flow when an external force is applied. When we talk about dynamic viscosity, we’re looking at how a fluid resists motion when an external force is applied. It’s like measuring how much effort it takes to stir honey with a spoon compared to water. Honey requires more force because it has a higher dynamic viscosity.

Dynamic viscosity is a measure of a fluid’s internal resistance to flow when an external force causes the layers of the fluid to slide past one another. It’s a way to quantify how “thick” or “resistant” a fluid is.

Imagine you have two plates with a layer of fluid between them. If you move the top plate while the bottom one stays still, the fluid between them will start to flow. The force you need to apply to the top plate to keep the fluid moving at a steady rate is related to the fluid’s dynamic viscosity.

The term “absolute” is used because dynamic viscosity is a fundamental property of the fluid itself, regardless of other conditions like temperature or pressure. It’s an intrinsic quality of the fluid that describes how it behaves under force.

The reason some fluids have higher dynamic viscosity than others comes down to the forces between their molecules. In fluids with high dynamic viscosity, like honey or oil, the molecules attract each other strongly, making it harder to move them apart. In fluids with low dynamic viscosity, like water or air, the molecules don’t cling to each other as much, so they can move more freely.

Dynamic viscosity is all about measuring how a fluid resists flow when an external force is applied. The formula for dynamic viscosity is:

\(\displaystyle \eta = \frac{\tau}{\gamma} \)

• (η) is the dynamic viscosity.
• (τ) is the shear stress, which is the force per unit area applied parallel to the fluid’s layers.
• (γ) is the shear rate, which is the rate at which the fluid layers are moving relative to each other.

To understand this formula, imagine you have a deck of cards and you’re trying to slide the top card off the deck. The force you apply to slide the card is like the shear stress (τ), and how quickly the card moves is like the shear rate (γ). The resistance you feel, which is the card’s reluctance to move, is similar to the fluid’s dynamic viscosity (η).

The unit of dynamic viscosity in the International System of Units (SI) is the pascal-second (Pa·s). It tells us how much force is needed to move a layer of fluid at a certain rate.

So, When you think of dynamic viscosity, picture how different fluids would resist your effort to move them. It’s a measure of how much a fluid likes to “stick to itself” and resist flowing freely when pushed or pulled.

Kinematic Viscosity

It measures the resistive flow of a fluid under the influence of gravity. When we talk about kinematic viscosity, we’re looking at a fluid’s resistance to flow under its weight, without any external forces except gravity. It’s like when you watch a drop of food coloring spread out in the water; it moves and mixes without you stirring it. That movement is influenced by the kinematic viscosity of the water.

Kinematic viscosity is a measure of how fast a fluid can flow under the influence of gravity. It’s calculated by dividing the fluid’s dynamic viscosity (its “thickness”) by its density (how much mass it has in a given volume). This gives us a number that tells us how freely the fluid flows on its own.

Imagine you have a race between two drops of liquid on a slope. One drop is water, and the other is honey. The water drop races down quickly, but the honey drop crawls slowly. This difference is because of their kinematic viscosities. Water has a low kinematic viscosity, so it flows fast. Honey has a high kinematic viscosity, so it flows slowly.

The formula for kinematic viscosity is pretty straightforward:

\(\displaystyle \nu = \frac{\mu}{\rho} \)

• (ν) is the kinematic viscosity.
• (μ) is the dynamic viscosity.
• (ρ) is the density of the fluid.

The units for kinematic viscosity are square meters per second (m²/s) in the SI system. It’s a way to express how much area a fluid will cover in a certain time under gravity alone.

Newtonian and Non-Newtonian Fluids

Newtonian Fluids:

Newtonian fluid’s viscosity remains constant regardless of the applied stress. Imagine you’re pouring a glass of water or blowing air through a straw. No matter how fast or slow you pour the water or blow the air, it feels the same, right? That’s because these fluids are Newtonian fluids.

Newtonian fluids are the “simple” fluids that behave exactly the way you’d expect. Their main characteristic is that their flow doesn’t change no matter how much force you apply. Whether you stir them gently or vigorously, their resistance to flow (viscosity) stays the same.

The behavior of Newtonian fluids is described by Newton’s law of viscosity. This law states that the shear stress (the force per unit area parallel to the fluid’s surface) is directly proportional to the shear rate (the rate at which the fluid layers move over each other). For Newtonian fluids, this relationship is linear, which means their viscosity is constant.

The mathematical expression for Newton’s law of viscosity is:

\(\displaystyle \tau = \mu \left( \frac{du}{dy} \right) \)

• (τ ) is the shear stress.
• (μ) is the fluid’s viscosity.
• \(\displaystyle \frac{du}{dy}\)is the shear rate or the velocity gradient.

Common examples of Newtonian fluids include water and air. No matter how you handle them, their viscosity remains constant.
Understanding Newtonian fluids is essential for many practical applications, from designing water pipes to understanding how blood flows in our veins. They are the standard against which other, more complex fluids are compared

Non-Newtonian Fluids:

Non-Newtonian Fluid viscosity changes when stress is applied. Have you ever played with slime or mixed cornstarch and water? If you have, you’ve encountered a non-Newtonian fluid. These fluids are fascinating because they don’t behave like typical liquids such as water or oil.

Non-Newtonian fluids are fluids that change their viscosity or “thickness” under stress. Unlike Newtonian fluids, which have a constant viscosity, non-Newtonian fluids can become thicker or thinner when you apply a force to them.

When you apply stress to non-Newtonian fluids—like hitting, shaking, or stirring them—they can behave in unexpected ways:

• Some become thicker and might even feel solid, like when you punch a tub of cornstarch and water mixture.
• Others become thinner and flow more easily, like ketchup that won’t come out of the bottle until you tap or squeeze it.

Types of Non-Newtonian Behaviors:

• Shear-Thinning: These fluids, like paint or blood, become less viscous when you stir or pump them.
• Shear-Thickening: These fluids, like the cornstarch mixture, become more viscous when you apply force.
• Thixotropic: They become less viscous over time under stress but return to their original state when the stress is removed.
• Rheopectic: The opposite of thixotropic, these fluids become more viscous over time under stress.

Non-Newtonian fluids are important for many real-world applications, like designing body armor that’s flexible but becomes hard on impact or making consumer products like toothpaste that flows easily out of the tube when squeezed but stays on your brush. So, non-Newtonian fluids are the rule-breakers of the fluid world, changing their behavior under different conditions.

Also Read: Pascal’s law

Viscosity Measurement

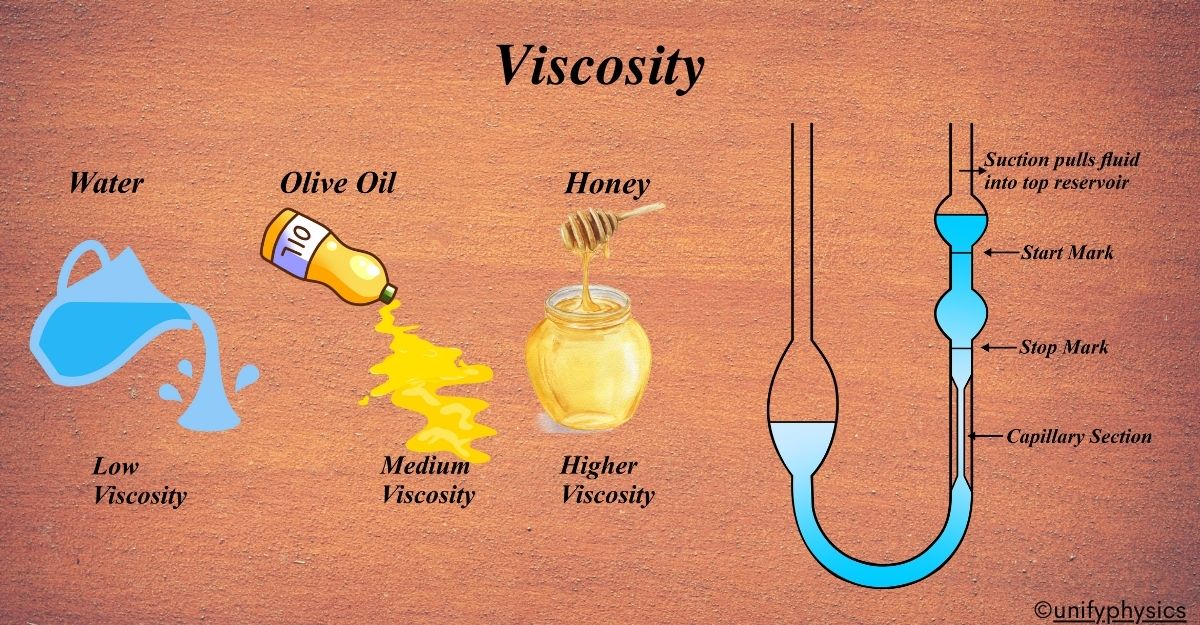
Viscosity can be measured using devices like the U-Tube Viscometer, where the time taken for a fluid to pass between two marks is recorded.

When scientists and engineers talk about measuring viscosity, they’re trying to figure out how thick or thin a fluid is and how it will behave under different conditions. It’s like measuring how fast honey drips off a spoon compared to water.

To measure the viscosity of a fluid, we use tools called viscometers. There are many types of viscometers, but they all have the same goal: to determine how resistant a fluid is to flow.

Common Methods of Viscosity Measurement:

• Capillary Viscometers: These are glass tubes with narrow sections. You time how long it takes for a fluid to pass through the narrow part. The faster it flows, the lower the viscosity.
• Rotational Viscometers: These have a cylinder inside a fluid. When the cylinder spins, it measures how much the fluid resists the motion. The more it resists, the higher the viscosity.
• Falling Sphere Viscometers: In this method, a sphere is dropped into the fluid, and the time it takes to fall a certain distance is measured. The slower the sphere falls, the higher the fluid’s viscosity.

The U-Tube Viscometer:

One specific type of viscometer is the U-Tube Viscometer. It’s shaped like a “U,” and you watch how the fluid moves in the tube when you tilt it. By measuring the time it takes for the fluid to flow from one side of the U to the other, you can calculate its viscosity.

You measure the time it takes for the liquid to pass from one mark on the tube to another. Using the time measured and the known density of the liquid, you can calculate the viscosity.

The U-Tube Viscometer is popular because it’s relatively easy to use and can give accurate measurements of a fluid’s viscosity. It’s especially useful in educational settings, like a 12th-grade physics lab, because it visually demonstrates the concept of viscosity and allows for hands-on learning.

The formula used to calculate viscosity with a U-Tube Viscometer involves the density of the fluid, the time taken for the fluid to flow between two marks and a constant that depends on the dimensions of the viscometer:

\(\displaystyle \eta = K \cdot \rho \cdot t \)

• (η) is the dynamic viscosity.
• (K) is the viscometer constant (depends on the viscometer’s dimensions).
• (ρ) is the density of the fluid.
• (t) is the time taken for the fluid to flow between the marks.

By using this method, students can get a practical understanding of how viscosity is measured and the factors that affect it. It’s a great way to bring the concept of viscosity to life in the classroom.

Measuring viscosity is crucial in many areas, like in the food industry to ensure the right texture of sauces, in manufacturing to make sure paints have the correct flow, and in medicine to understand the flow of blood through our veins. Measure viscosity helps us control and utilize the flow properties of fluids in everything from cooking to car engines.

Factors Affecting Viscosity

Viscosity, the measure of a fluid’s resistance to flow, is influenced by a variety of factors that affect its internal structure and behavior.Understanding these factors is essential for predicting and controlling fluid flow in various applications, from industrial processes to biological systems.

Temperature

For liquids, viscosity decreases with an increase in temperature. For gases, it increases with temperature. When we talk about the effect of temperature on viscosity, we’re looking at how heat changes the way fluids flow. Think of viscosity as the “thickness” or “stickiness” of a fluid. Now, what happens when you heat something sticky like honey? It becomes runnier, right? That’s because heat generally makes liquids less viscous—they flow more easily.

• For Liquids: When you increase the temperature, the molecules in the liquid move faster. This increased movement means that the molecules don’t “stick” to each other as much, so the liquid flows more freely. Essentially, the intermolecular forces that contribute to viscosity are weakened by the added heat.
• For Gases: It’s a bit different. When gases are heated, their viscosity actually increases. This is because the faster-moving molecules collide more often, which leads to an increase in the momentum transfer between the layers of gas, making it more resistant to flow.

Examples:

• Engine Oil: In cold weather, the oil in a car engine is thicker (more viscous), which is why engines can be harder to start. As the engine warms up, the oil becomes thinner (less viscous) and flows better.
• Syrup: Cold syrup pours slowly because it’s more viscous. When heated, it pours quickly because its viscosity decreases.

So, remember, when it comes to viscosity, temperature is like a magic wand—it can make fluids flow faster or slower, depending on whether you’re dealing with a liquid or a gas.

Pressure

Increasing pressure can increase the viscosity of a fluid. When we talk about pressure and its effect on viscosity, we’re considering how squeezing or compressing a fluid changes its flow characteristics.

Imagine you have a tube of toothpaste. When you squeeze the tube (which increases the pressure), the toothpaste comes out more slowly if it’s thick. This is similar to how pressure can affect the viscosity of fluids.

For liquids, increasing pressure usually means the molecules are forced closer together. This can make it harder for the molecules to move past each other, which can increase the viscosity. However, this effect is generally small unless the pressure is increased by a lot. For most liquids, especially under conditions we encounter in everyday life, the change in viscosity with pressure is not significant.

How Pressure Affects Gases: Gases behave differently. Under normal conditions, the viscosity of gases is independent of pressure. But when the ideal gas model doesn’t apply—like at very low temperatures or very high pressures—the viscosity of gases can decrease as pressure increases. This happens because the molecules are moving faster, which can lead to a decrease in resistance to flow.

Real-World Implications: Understanding how pressure affects viscosity is important in various fields, such as:

• Aerospace: Predicting how air will flow over a plane’s wings at high altitudes where pressure is low.
• Subsea Engineering: Knowing how oil will flow through pipelines at the bottom of the ocean where pressures are extremely high.

So, while pressure does affect the viscosity of both liquids and gases, it’s often a secondary factor compared to temperature. For liquids, it’s only under extreme pressure that we see a noticeable increase in viscosity. For gases, viscosity can decrease with pressure, but again, this is usually under conditions that are not typical of everyday experiences.

Dependence of Viscosity

Viscosity depends on the fluid’s molecular composition and the intermolecular forces present. When you think about viscosity, remember it’s not just about being thick or thin; it’s about how all these different factors come together to influence a fluid’s flow. It’s a bit like a dance, where the molecules, temperature, pressure, and other elements all have to move in harmony to create the fluid’s unique flow characteristics.

Viscosity isn’t just a random property; it depends on several factors that can change how a fluid behaves. When we talk about the dependence of viscosity, we’re looking at what influences a fluid’s resistance to flow.

• Molecular Composition: The type of molecules in a fluid and how they’re arranged play a big role in viscosity. For example, honey has more complex molecules than water, which is why it’s thicker and has a higher viscosity.
• Intermolecular Forces: The forces between molecules—like how much they attract or repel each other—also affect viscosity. Stronger intermolecular forces mean higher viscosity because the molecules don’t want to move past each other easily.
• Temperature: As we’ve discussed, temperature is a big factor. For liquids, higher temperatures usually mean lower viscosity because the molecules move faster and can overcome their attractions more easily. For gases, it’s the opposite; higher temperatures can increase viscosity.
• Pressure: Pressure can also affect viscosity, especially in liquids. When you compress a liquid, you’re pushing its molecules closer together, which can make it flow less easily. However, this effect is usually small unless the pressure changes are very large.
• The Presence of Additives: Sometimes, other substances are added to fluids to change their viscosity. For example, adding thickening agents to paint can increase its viscosity, making it spread more smoothly without dripping.

Applications of Viscosity

Viscosity has numerous applications, such as in lubricants to reduce wear and tear, in culinary arts for syrup and sauce consistency, and in industrial processes where fluid flow is critical. Here are some examples where understanding viscosity is essential:

• Lubricants: The oils used in car engines and heavy machinery need to have the right viscosity. If they’re too thick, they won’t flow well; if they’re too thin, they won’t lubricate effectively. Knowing how viscosity changes with temperature helps in selecting the right oil.
• Medical Field: The viscosity of blood is a critical factor in diagnosing and treating certain medical conditions. It affects how blood circulates through arteries and veins.
• Food Industry: When making foods like dosas, chapatis, or syrups, the viscosity of the batter or syrup is important for the right texture and consistency.
• Paints and Inks: High-viscosity liquids are used in paints to prevent dripping and ensure a smooth coat. Similarly, the ink in pens must have the right viscosity to flow smoothly without leaking.
• Industrial Applications: Viscosity is crucial in manufacturing processes where fluid flow is involved. For example, it’s important in the design of hydraulic systems, such as brakes, where a high-viscosity fluid can effectively transfer force.
• Scientific Research: Experiments like the famous oil drop experiment by Millikan, which helped determine the charge of an electron, relied on an understanding of viscosity.
• Consumer Products: Everyday items like shampoo, lotions, and creams have specific viscosities to make them easy to spread but not too runny.

Solved Examples

Example 1: A fluid has a viscosity of (0.01 Ns/m²) and experiences a shear stress of (100 Ns/m²). Calculate the rate of shear in the fluid.

Solution: The rate of shear (\(\displaystyle\dot{\gamma} \)) can be calculated using the formula:

\(\displaystyle \dot{\gamma} = \frac{\text{Shear stress}}{\text{Viscosity}} \)
\(\displaystyle \dot{\gamma} = \frac{100}{0.01} = 10000 \, \text{s}^{-1} \)

So, the rate of shear in the fluid is (10000 s^-1).

Example 2: A fluid has a viscosity of (0.1 Ns/m²) and experiences a shear rate of (500 s^-1). Calculate the shear stress experienced by the fluid.

Solution: The shear stress (τ) can be calculated using the formula:

\(\displaystyle \tau = \text{Viscosity} \times \text{Shear rate} \)
\(\displaystyle\tau = 0.1 \times 500 = 50 \, \text{Ns/m}^2 \)

So, the shear stress experienced by the fluid is (50 Ns/m²).

Example 3: The viscosity of a liquid decreases from 20 Pa·s to 10 Pa·s as the temperature increases from 25°C to 50°C. Calculate the rate of change of viscosity with temperature.

Solution: To calculate the rate of change of viscosity with temperature, we can use the formula for the rate of change of a quantity:

\(\displaystyle \text{Rate of change} = \frac{\text{Change in quantity}}{\text{Change in temperature}} \)

Given:

• Initial viscosity (µ₁) = 20 Pa·s
• Final viscosity (µ₂) = 10 Pa·s
• Initial temperature (T₁) = 25°C
• Final temperature (T₂) = 50°C

First, let’s find the change in viscosity and change in temperature:

Change in viscosity \(\displaystyle( \Delta \mu ) = ( \mu_2 – \mu_1 ) = 10 Pa·s – 20 Pa·s = -10 Pa·s\)

Change in temperature \(\displaystyle( \Delta T ) = ( T_2 – T_1 ) = 50°C – 25°C = 25°C\)

Now, we can calculate the rate of change of viscosity with temperature:

\(\displaystyle \text{Rate of change} = \frac{\Delta \mu}{\Delta T} \)

\(\displaystyle \text{Rate of change} = \frac{-10 \, \text{Pa·s}}{25 \, \text{°C}} \)

\(\displaystyle \text{Rate of change} = -0.4 \, \text{Pa·s/°C} \)

So, the rate of change of viscosity with temperature is ( -0.4 Pa·s/°C).

Example 4: Water flows through a pipe with a radius of 0.02 m at a velocity of 3 m/s. If the dynamic viscosity of water is \(\displaystyle1 \times 10^{-3}\) Pa·s, calculate the shear stress on the pipe wall.

Solution: To calculate the shear stress on the pipe wall, we can use the formula for shear stress (τ) in a fluid flow:

\(\displaystyle \tau = \mu \frac{du}{dy} \)

Given:

• Dynamic viscosity of water (µ) = \(\displaystyle 1 \times 10^{-3}\) Pa·s
• The radius of the pipe (r) = 0.02 m
• Velocity of water (v) = 3 m/s

First, let’s find the velocity gradient (\(\displaystyle \frac{du}{dy}\)). Since the flow is laminar and through a cylindrical pipe, the velocity profile is linear, and the velocity gradient is constant.

The velocity gradient can be calculated using the formula:

\(\displaystyle \frac{du}{dy} = \frac{v}{r} \)

\(\displaystyle \frac{du}{dy} = \frac{3}{0.02} \)
\(\displaystyle \frac{du}{dy} = 150 \, \text{s}^{-1}\)

Now, we can calculate the shear stress (τ):

\(\displaystyle \tau = \mu \frac{du}{dy} \)
\(\displaystyle \tau = (1 \times 10^{-3}) \times 150 \)
\(\displaystyle \tau = 0.15 \, \text{Pa} \)

So, the shear stress on the pipe wall is (0.15 Pa).

FAQs