The concept of pressure was developed in the 17th century by scientists like Blaise Pascal and Evangelista Torricelli. They observed that fluids exert force over an area and related this to atmospheric phenomena.
In 1643, Evangelista Torricelli, an Italian mathematician and physicist, conducted a groundbreaking experiment. He inverted a mercury-filled tube into a dish of mercury and observed that some of the mercury did not spill out as expected. Instead, it left a vacuum at the top and the mercury column settled at a particular height. This was the first time atmospheric pressure was demonstrated and measured. Torricelli’s experiment led to the development of the barometer, an instrument to measure atmospheric pressure.
Following Torricelli’s work, Blaise Pascal, a French mathematician, physicist, and inventor, furthered the understanding of pressure. He articulated Pascal’s Law, which states that pressure applied to a fluid is transmitted undiminished throughout the fluid. This principle laid the foundation for hydraulics and has numerous applications in modern technology.
Even before Pascal, Simon Stevin, a Flemish mathematician and engineer, had worked with the concept of pressure through his studies of hydrostatics. He discovered the hydrostatic paradox, which showed that the pressure at the bottom of a container filled with liquid depends only on the height of the liquid and not on the shape of the container.
The modern definition of pressure as the force per unit area was developed from these early experiments and theories. It was understood that whether it’s the weight of the air above us or the force exerted by a gas in a container, pressure describes how these forces are distributed over a surface.
What is Pressure?
Pressure is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. It’s like how tightly the particles of a substance are pushing against each other.
Imagine you’re standing in a crowded room. The more people there are, the more you feel pushed from all sides. Now, if everyone in the room were to move closer together, that push would feel stronger. This is similar to how pressure works.
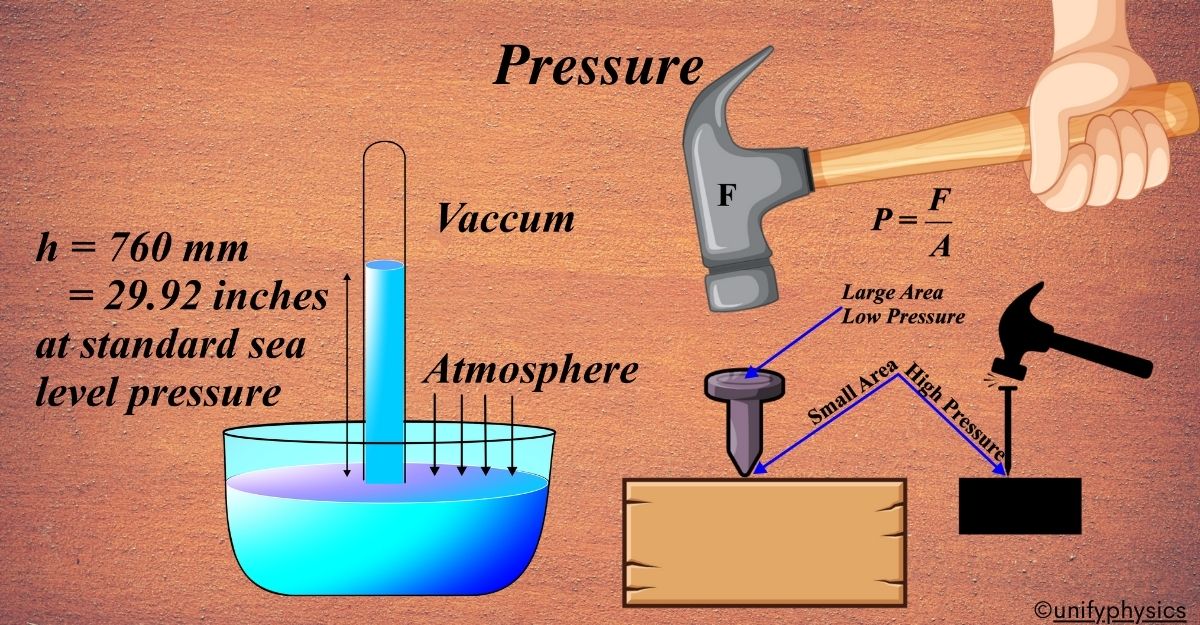
When you use a hammer to drive a nail into a wooden block, you’re exerting force on the nail head, which then applies pressure to the surface of the wood. Pressure is defined as force per unit area, so the force you apply with the hammer is spread out over the area of the nail head that contacts the wood.
Imagine you’re using a small finishing nail and tapping it lightly with a small hammer. Because the force is spread out over a small area, the pressure exerted on the wood is relatively low. As a result, the nail may not penetrate the wood very deeply, and the impact on the wood surface might be minimal.

Now, let’s consider using a larger nail and a heavier hammer to drive it into the same wooden block. The larger nail has a larger surface area, and the heavier hammer delivers more force. As a result, the pressure exerted on the wood is higher. With this increased pressure, the nail can penetrate deeper into the wood, and the impact on the wood surface is more significant.
In both cases, the pressure exerted by the hammer and nail is crucial for driving the nail into the wood. However, the amount of pressure depends on factors such as the force applied by the hammer, the surface area of the nail head, and the hardness of the wood.
This example illustrates how pressure is applied in everyday situations and how it influences the interaction between objects, like a hammer and a nail, and the surfaces they come into contact with.
In physics, pressure is the measure of the force exerted on a surface area. Here’s a simple breakdown:
- Force: Think of it as a push or a pull. When you press your hand against a wall, you’re applying force to it.
- Surface Area: This is the part of the wall where your hand is making contact. If you use just your fingertip, the area is small, but if you use your entire palm, the area is larger.
Now, pressure is what you get when you divide the force by the area over which it’s applied. It’s like spreading the force out over a space. The smaller the area, the more pressure you feel, just like the crowded room example. Pressure is calculated using a simple formula:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{P = \frac{F}{A} }} \end{equation}\)
- (P) stands for pressure,
- (F) is the force applied,
- (A) is the area over which the force is distributed.
Think of it like this: if you press down on a sponge with your hand, you’re applying a force. The area of the sponge where your hand touches is the surface area. Now, if you press down with the same force but only use one finger, the sponge will compress more because the force is concentrated over a smaller area. That’s pressure!
The standard unit of pressure in the International System of Units (SI) is the Pascal (Pa). One pascal is equal to one newton per square meter (N/m²). It’s named after Blaise Pascal, the French scientist who did a lot of early work on pressure. While the pascal is the SI unit, pressure is also commonly measured in:
- Atmospheres (atm): Based on the average atmospheric pressure at sea level.
- Bars: Where 1 bar is approximately equal to the atmospheric pressure at sea level.
- Pounds per square inch (psi): Often used in the U.S.
To visualize this, imagine you have a book resting on a table. If the book has an area of 1 m² and you push down on it with a force of 1 newton, you’re applying a pressure of 1 pascal on the table’s surface.
So, if you apply the same force over a smaller area, you get a higher pressure. That’s why a sharp knife cuts better than a blunt one; it applies the same force over a smaller area, resulting in higher pressure and a cleaner cut.
So, pressure is all about how spread out a force is. The more concentrated the force, the higher the pressure, and that’s a concept that pops up everywhere, from weather systems to car tires, and even in the human body with blood pressure.
Types of Pressure
Atmospheric Pressure
Atmospheric pressure is the force exerted by the weight of the air in the Earth’s atmosphere. It’s like the air is a giant ocean above us, and just like water pressure increases with depth, the air pressure is highest at the Earth’s surface because of all the air above pressing down.
Atmospheric pressure is measured using a barometer. A common type of barometer uses mercury and measures the height of the mercury column, which rises or falls as the atmospheric pressure changes. Atmospheric pressure affects everything from the weather to how we breathe. High and low-pressure systems influence the climate and can determine if the day is sunny or if a storm is coming.
Imagine a long glass tube, closed at one end and filled with mercury, being inverted into a trough of mercury.
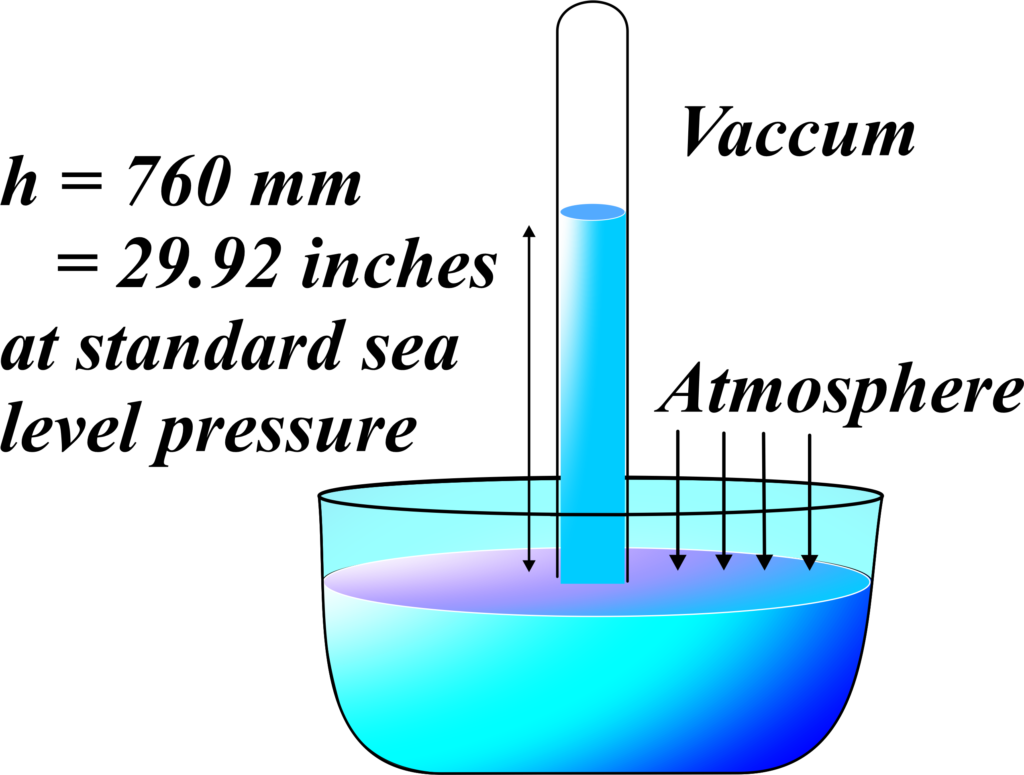
As the tube is inverted, some of the mercury in the tube will flow out due to gravity, but not all of it.
Instead, a column of mercury remains suspended in the tube, with its height determined by the balance between the downward force of gravity and the upward force of atmospheric pressure.
The height of the mercury column in the tube represents the atmospheric pressure at the location where the barometer is situated. The higher the atmospheric pressure, the taller the mercury column will be, and vice versa.
- Atmospheric pressure pushes down on the surface of the mercury in the trough, forcing mercury up into the tube.
- The weight of the mercury column in the tube exerts a downward force due to gravity.
- When these two forces reach equilibrium, the height of the mercury column stops changing, indicating the atmospheric pressure at that location.
The mercury barometer is an essential tool for measuring atmospheric pressure and has been widely used in meteorology and weather forecasting. It demonstrates how atmospheric pressure acts on fluids and provides a practical method for quantifying this pressure using the height of a mercury column.
The standard atmospheric pressure at sea level is typically around 760 millimeters of mercury (mmHg), or 101.3 kilopascals (kPa). This means that the height of the mercury column in a mercury barometer at sea level will be approximately 760 mm.
At sea level, the standard atmospheric pressure is 101,325 pascals (Pa) or 1 atmosphere (atm). This is the average pressure at sea level on Earth. As you go higher up, like when climbing a mountain or flying in an airplane, the atmospheric pressure decreases because there’s less air above you. This is why it can be harder to breathe at high altitudes.
Examples:
- Weather Forecasting: Meteorologists use atmospheric pressure to predict weather changes.
- Breathing: Our lungs work with the atmospheric pressure to help us breathe.
- Cooking: High-altitude cooking requires adjustments because water boils at lower temperatures due to lower atmospheric pressure.
Absolute Pressure
Absolute Pressure is the total pressure exerted on a system, regardless of external factors. It’s the sum of all pressures at a certain point, including the pressure of the atmosphere if the system is not sealed.
Think of a sealed can of soda. Inside, there is pressure from the carbonated liquid pushing outwards. This is the pressure inside the can. Now, if we could measure this pressure without the influence of the air around the can, that would be the absolute pressure.
Absolute pressure is crucial in calculations where the presence of air is a factor, such as in:
- Scuba Diving: Divers need to know the absolute pressure underwater to avoid decompression sickness.
- Industrial Processes: Many systems need to maintain a certain absolute pressure to function correctly.
To measure absolute pressure, we use an absolute pressure gauge or sensor, which gives us the reading directly. The formula for absolute pressure (Pabs) is:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{P_{abs} = P_{gauge} + P_{atm} }} \end{equation}\)
- (Pabs) is the absolute pressure,
- (Pgauge) is the gauge pressure (pressure measured by a gauge),
- (Patm) is the atmospheric pressure.
The Zero Reference Point:
When we talk about absolute pressure, we’re diving into the heart of fluid mechanics. Imagine you’re measuring the height of a mountain. To do this accurately, you need a starting point—a baseline from which all measurements begin. In the world of pressure, we have a similar reference point: the perfect vacuum.
What’s a Perfect Vacuum?
A perfect vacuum is a space completely devoid of matter—no air, no particles, just emptiness. It’s the ultimate absence of pressure. Think of it as standing in outer space, far away from any planets or stars. There, the pressure is precisely zero.
Using a perfect vacuum as our reference point allows us to measure the true pressure exerted by a fluid without any external influences. It’s like measuring the height of a mountain from sea level rather than from a hill. Sea level serves as a universally accepted zero point for altitude, just as the vacuum does for pressure.
So, what exactly is absolute pressure? It’s the total pressure exerted by a fluid (whether liquid or gas) on a surface. When we measure absolute pressure, we’re considering both the pressure due to the fluid itself and any additional atmospheric pressure. It’s the real deal—the pressure without any compromises.
Example: Imagine you have a sealed container. The pressure inside that container, measured relative to the perfect vacuum, is the absolute pressure. It’s not influenced by the surrounding air pressure. If you were in that outer space vacuum, a pressure gauge designed for absolute pressure would read zero because there’s no pressure being exerted.
The zero reference point for absolute pressure is crucial. It ensures that when we talk about the pressure of a gas in a tank or the immense pressure deep in the ocean, we’re measuring it against a universal standard—the perfect vacuum. It’s a consistent way to understand and compare pressures across different contexts.
Differential Pressure
Differential Pressure is the difference in pressure between two points in a fluid system. It’s like comparing the pressure at the bottom of a hill to the pressure at the top; the difference between the two is the differential pressure.
Imagine you have two balloons, one inflated more than the other. The balloon with more air has higher pressure inside. If you connected the two balloons with a tube, air would flow from the higher-pressure balloon to the lower-pressure one until the pressures equalize. The initial difference in pressure is what we call differential pressure.
Differential pressure is used to measure flow rate, level, and even filtering status in various systems. For example:
- Flow Rate: In pipes, differential pressure helps determine how much fluid is flowing from one point to another.
- Level Measurement: In tanks, it can tell us how full a tank is based on the pressure difference between the top and bottom.
To measure differential pressure, we use a device called a differential pressure gauge. This gauge has two ports: one connected to the high-pressure point and the other to the low-pressure point. The gauge shows the pressure difference between these two points.
There isn’t a single formula for differential pressure because it’s simply the difference between two pressures. If we denote (P1) as the pressure at point one and P2) as the pressure at point two, the differential pressure (Pdiff) is:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ P_{diff} = P_{1} – P_{2}}} \end{equation}\)
Examples:
- Heating Systems: Differential pressure is monitored to ensure that hot water or steam is circulating properly.
- Airplanes: Pilots use differential pressure to check the cabin’s pressurization.
Differential pressure is a key concept in understanding how fluids move and behave in different environments. It’s a measure of the push that drives fluids from areas of high pressure to areas of low pressure, and it’s essential for the functioning of many systems we rely on every day.
Gauge Pressure
Gauge Pressure is the pressure of a fluid (liquid or gas) measured relative to the atmospheric pressure. It’s the extra pressure in a system compared to the air around us.
Imagine you’re inflating a bicycle tire. The pressure gauge on the pump shows how much pressure is in the tire. This reading is the gauge pressure, and it doesn’t include the atmospheric pressure that’s already pushing on everything at the surface of the Earth.
While absolute pressure measures the total pressure (including atmospheric pressure), gauge pressure measures only the pressure above the atmospheric pressure. If the gauge reads zero, it means the pressure inside the system is the same as the atmospheric pressure.
Gauge pressure is useful because it tells us the pressure that’s being applied by a device or system, like the pressure from the air in a tire or the steam in a boiler.
Gauge pressure is measured using a pressure gauge, which is calibrated to read zero in the Earth’s atmosphere. It’s like setting the scale to zero before weighing something; it gives you the actual weight without any extras. The formula for gauge pressure (Pgauge) is:
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{P_{gauge} = P_{abs} – P_{atm} }} \end{equation}\)
- (Pgauge) is the gauge pressure,
- (Pabs) is the absolute pressure,
- (Patm) is the atmospheric pressure.
Examples:
- Car Tires: The pressure indicated by a tire pressure gauge is the gauge pressure.
- Air Compressors: They often use gauge pressure to indicate how much pressure is being applied to the air they’re compressing.
Variation of Pressure with Depth
In fluids, pressure increases with depth due to the weight of the fluid above. When you dive into a swimming pool, you might notice that your ears start to feel a bit funny the deeper you go. This is because of an increase in pressure with depth.
Imagine a column of water in the ocean. The deeper you go, the more water is above you, and since water has weight, it exerts more force on the areas below. This weight causes the pressure to increase as you go deeper. The pressure at a certain depth in a fluid is given by the formula:
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{P = P_{0} + \rho gh }} \end{equation}\)
- (P) is the pressure at depth,
- (P0) is the atmospheric pressure at the surface,
- (ρ) is the density of the fluid,
- (g) is the acceleration due to gravity,
- (h) is the depth below the surface.
Think of a stack of books. The book at the bottom has to support the weight of all the books above it, so it’s under more pressure. Similarly, at greater depths in a fluid, the pressure is higher because of the weight of the fluid above.
Examples:
- Scuba Diving: Divers need to be aware of the increased pressure with depth to avoid health issues like decompression sickness.
- Engineering: Structures like dams and submarines must be designed to withstand the pressure at the depths they will encounter.
Derivation:
Imagine a column of water in the ocean. The deeper you go, the more water is above you, and thus, the greater the weight that presses down. Take a small vertical column of fluid with a cross-sectional area (A) and a height (h) below the surface. The volume (V) of the fluid in the column is the area (A) times the height (h):
\(\displaystyle V = A \cdot h \)
The mass (m) of the fluid is its density (ρ) times the volume (V):
\(\displaystyle m = \rho \cdot V \)
Substituting the volume from the previous step:
\(\displaystyle m = \rho \cdot A \cdot h \)
The weight (W) of the fluid is its mass (m) times the acceleration due to gravity (g ):
\(\displaystyle W = m \cdot g \)
Substituting the mass from the previous step:
\(\displaystyle W = \rho \cdot A \cdot h \cdot g \)
The pressure (P) at the bottom of the column is the weight (W) divided by the area (A):
\(\displaystyle P = \frac{W}{A} \)
Substituting the weight from the previous step:
\(\displaystyle P = \frac{\rho \cdot A \cdot h \cdot g}{A} \)
The area (A) cancels out:
\(\displaystyle P = \rho \cdot h \cdot g \)
Finally, we must remember that this pressure is in addition to the atmospheric pressure (P0) already present at the surface. So, the total pressure (P) at depth (h) is:
\(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{P = P_{0} + \rho \cdot h \cdot g }} \end{equation}\)
This equation tells us that the deeper you go into a fluid, the greater the pressure will be, and it increases linearly with depth. Engineers use this equation to design submarines and underwater structures to withstand pressure at certain depths.
Also Read: Stress And Strain
Factors Affecting Pressure
Pressure in fluids isn’t just a random number; it’s affected by specific factors that can change how much pressure is exerted. Here are the main factors:
Density (ρ): Density is the mass of fluid per unit volume. The denser a fluid is, the more mass it has in a given space, and the higher the pressure it can exert.
- Example: Think of a bag filled with cotton versus a bag of the same size filled with sand. The sand is denser and will feel heavier, exerting more pressure on the ground.
Gravity (g): Gravity is the force that pulls everything towards the center of the Earth. It affects how much the fluid’s weight contributes to the pressure.
- Example: On Earth, gravity is ( 9.8, m/s2), but if you were on a planet with stronger gravity, the pressure at the bottom of a pool would be greater because the water’s weight would increase.
Depth (h): Depth is how far below the surface of the fluid you are. The deeper you go, the more fluid is above you, and the greater the pressure.
- Example: Diving into the deep end of a pool versus the shallow end. In the deep end, you’ll feel more pressure on your ears because there’s more water above you.
Atmospheric Pressure (P0): Atmospheric Pressure is the pressure exerted by the weight of the air above the fluid. It adds to the overall pressure experienced by the fluid.
- Example: At higher altitudes, atmospheric pressure is lower, so the total pressure in a fluid will also be lower compared to sea level.
Applications of Pressure in Daily Life
- Cutting and Piercing Tools: The sharp edges of knives, scissors, and needles have a very small surface area. When a force is applied to them, the pressure exerted is high, making it easier to cut or pierce through materials.
- Hydraulic Systems: These systems use pressure to multiply force. By applying pressure to a small area, a larger force can be exerted on a bigger area, like in hydraulic brakes and lifts.
- Weather Patterns: Atmospheric pressure plays a significant role in meteorology. High and low-pressure systems influence weather conditions, such as storms and clear skies.
- Aerodynamics: Air pressure is crucial in flight. The pressure difference above and below the wings of an airplane provides the lift needed for flight.
- Drinking with Straws: When you drink through a straw, you create a pressure difference. The lower pressure inside the straw causes the liquid to rise and flow into your mouth.
- Medical Devices: Blood pressure monitors and syringes rely on pressure. In syringes, a decrease in pressure draws fluid in, while blood pressure cuffs measure the pressure exerted by blood in the arteries.
- Sports Equipment: The bounce of a basketball or soccer ball depends on the air pressure inside. Adjusting this pressure changes how the ball behaves during play.
- Cooking: Pressure cookers use steam pressure to cook food faster. The high pressure inside raises the boiling point of water, cooking food more quickly.
- Tires: The pressure of the air inside tires supports the weight of vehicles and affects traction, handling, and fuel efficiency.
- Diving: Scuba divers must understand the pressure to safely explore underwater environments. The pressure increases with depth, affecting buoyancy and the risk of decompression sickness.
These examples show how pressure is not just a theoretical concept but a practical one that influences many aspects of our daily lives and the technology we use.
Solved Examples
Example 1: Calculate the pressure exerted by a force of (500 N) acting on an area of (0.1m2).
Solution: Given;
- Force, (F = 500 N)
- Area, (A = 0.1m2)
Pressure (P) is given by the formula:
\(\displaystyle P = \frac{F}{A} \)
\(\displaystyle P = \frac{500}{0.1} \)
\(\displaystyle P = 5000 \, \text{Pa} \)
So, the pressure exerted is (5000 Pa).
Example 2: Explain the difference between absolute pressure and gauge pressure.
Solution: The main difference is in their reference points: absolute pressure is measured relative to a perfect vacuum, while gauge pressure is measured relative to atmospheric pressure.
- Absolute Pressure: Absolute pressure uses a perfect vacuum as its zero reference point. In other words, it measures the total pressure exerted by a fluid (liquid or gas) relative to a complete absence of pressure. This means that absolute pressure includes atmospheric pressure in addition to the pressure exerted by the fluid itself. It is often used in scientific and engineering contexts where precise pressure measurements are required, such as in vacuum systems or deep-sea exploration.
- Gauge Pressure: Gauge pressure, on the other hand, uses atmospheric pressure as its zero reference point. It measures the pressure exerted by a fluid relative to atmospheric pressure, which is approximately 101.3 kPa (kilopascals) or 14.7 psi (pounds per square inch) at sea level. Gauge pressure does not account for atmospheric pressure; instead, it indicates the pressure above or below atmospheric pressure. This type of pressure measurement is commonly used in everyday applications like tire pressure gauges, where the pressure displayed is the pressure above atmospheric pressure.
Example 3: A submarine is (50 m) below the surface of the ocean. Calculate the total pressure exerted on the submarine, considering atmospheric pressure to be \(\displaystyle1.013 \times 10^5 \, \text{Pa}\) and density of seawater to be \(\displaystyle1025 \, \text{kg/m}^3\). (Take (g = 9.8 m/s2)
Solution: The total pressure (Ptotal) on the submarine can be calculated using the formula:
\(\displaystyle P_{\text{total}} = P_{\text{atm}} + \rho g h \)
\(\displaystyle P_{\text{total}} = 1.013 \times 10^5 + (1025 \times 9.8 \times 50) \)
\(\displaystyle P_{\text{total}} = 1.013 \times 10^5 + 501250 \)
\(\displaystyle P_{\text{total}} = 1.51425 \times 10^5 \, \text{Pa} \)
So, the total pressure exerted on the submarine is \(\displaystyle 1.51425 \times 10^5 \, \text{Pa}\).
Example 4: Explain how pressure varies with depth in a fluid.
Solution: Pressure varies with depth in a fluid according to a fundamental principle known as Pascal’s Law or Pascal’s Principle. This principle states that the pressure exerted at any point in a fluid at rest is equal in all directions and increases with depth due to the weight of the fluid above.
Imagine diving into a swimming pool. As you descend deeper into the water, you feel an increase in pressure on your ears and body. This increase in pressure occurs because the weight of the water above you exerts a force downwards, which translates into an increase in pressure as you go deeper.
Mathematically, the relationship between pressure and depth in a fluid is given by the equation:
\(\displaystyle P = P_{0} + \rho \cdot g \cdot h \)
This equation shows that pressure increases linearly with depth. The deeper you go into the fluid, the greater the pressure becomes due to the increased weight of the fluid above exerting a greater force.
Example 5: Explain how the shape and size of a container affect the pressure exerted by a fluid.
Solution: The shape and size of a container can significantly affect the pressure exerted by a fluid within it. This is due to the fundamental principles of fluid mechanics, including Pascal’s Law and Archimedes’ Principle.
Shape of the Container:
- Pascal’s Law states that pressure exerted at any point in a fluid at rest is transmitted equally in all directions. Therefore, the shape of the container influences how pressure is distributed within the fluid.
- In a container with a narrow opening or a smaller cross-sectional area, the same amount of fluid exerts pressure over a smaller area, resulting in higher pressure. Conversely, in a container with a wider opening or a larger cross-sectional area, the pressure is distributed over a larger area, resulting in lower pressure.
- For example, consider a water bottle with a narrow neck and a wide base. The pressure at the bottom of the bottle is higher compared to the pressure at the top due to the weight of the water above. However, the pressure is more evenly distributed in a wider container.
Size of the Container:
- The size of the container affects the volume of fluid it can hold and, consequently, the weight of the fluid exerting pressure.
- A larger container holds more fluid, resulting in a greater weight of fluid pressing down on the bottom surface and, therefore, a higher pressure at the bottom.
- Conversely, a smaller container holds less fluid, resulting in less weight pressing down and lower pressure.
- For instance, consider a bathtub compared to a small bucket. The pressure exerted by the water at the bottom of the bathtub is greater due to the larger volume of water compared to the pressure at the bottom of the bucket with a smaller volume of water.
The shape and size of a container influence the distribution and magnitude of pressure exerted by a fluid.
Example 6: A diver is swimming (15 m) below the surface of a lake. Calculate the gauge pressure experienced by the diver. (Take atmospheric pressure to be \(\displaystyle 1.013 \times 10^5 \, \text{Pa})\)
Solution: Gauge pressure (Pgauge) is the difference between total pressure and atmospheric pressure. Using the formula for total pressure:
\(\displaystyle P_{\text{total}} = P_{\text{atm}} + \rho g h \)
\(\displaystyle P_{\text{gauge}} = P_{\text{total}} – P_{\text{atm}} \)
\(\displaystyle P_{\text{gauge}} = (1.013 \times 10^5 + 1025 \times 9.8 \times 15) – 1.013 \times 10^5 \)
\(\displaystyle P_{\text{gauge}} = (1.013 \times 10^5 + 150375) – 1.013 \times 10^5 \)
\(\displaystyle P_{\text{gauge}} = 251845 \, \text{Pa} \)
So, the gauge pressure experienced by the diver is (251845 Pa).
FAQs
What exactly is pressure, and how is it defined in physics?
Pressure is a measure of the force applied per unit area. In physics, it’s defined as the force acting perpendicular to a surface divided by the area over which the force is applied. Mathematically, pressure (P) is expressed as \(\displaystyle P = \frac{F}{A}\).
Can you explain the different types of pressure encountered in everyday life?
There are several types of pressure, including atmospheric pressure (the pressure exerted by the weight of air molecules in the Earth’s atmosphere), hydraulic pressure (pressure exerted by fluids), and osmotic pressure (pressure exerted by a solution to prevent the influx of water across a semipermeable membrane).
How does pressure vary with depth in a fluid, and what principle governs this variation?
Pressure in a fluid increases with depth due to the weight of the fluid above pushing down. This variation is governed by Pascal’s principle, which states that in a confined fluid at rest, the pressure exerted at any point is transmitted equally in all directions.
What factors affect the pressure experienced by an object submerged in a fluid?
Several factors influence the pressure experienced by an object submerged in a fluid, including the density of the fluid, the acceleration due to gravity, and the depth of submersion. Additionally, the shape and orientation of the object relative to the fluid flow can also affect the pressure distribution.
How does the pressure change when moving from sea level to higher altitudes, and why?
As altitude increases, atmospheric pressure decreases. This is because the density of air decreases with altitude, leading to fewer air molecules exerting force per unit area. Therefore, at higher altitudes, there is less atmospheric pressure compared to sea level.
What is gauge pressure, and how does it differ from absolute pressure?
Gauge pressure is the pressure measured relative to atmospheric pressure. It represents the pressure above or below atmospheric pressure. Absolute pressure, on the other hand, includes atmospheric pressure as a reference point and is measured relative to a perfect vacuum. In other words, absolute pressure is the total pressure, including atmospheric pressure, while gauge pressure only measures the pressure above or below atmospheric pressure.
How does pressure affect the boiling point of a liquid, and are there any exceptions to this relationship?
Pressure affects the boiling point of a liquid by altering the equilibrium between the liquid and its vapor phase. At higher pressures, the boiling point increases because it requires more energy to overcome the increased pressure and reach the vapor phase. Conversely, at lower pressures, the boiling point decreases. However, there are exceptions, such as water, which exhibits anomalous behavior at very high pressures, where the boiling point may increase instead of decrease.