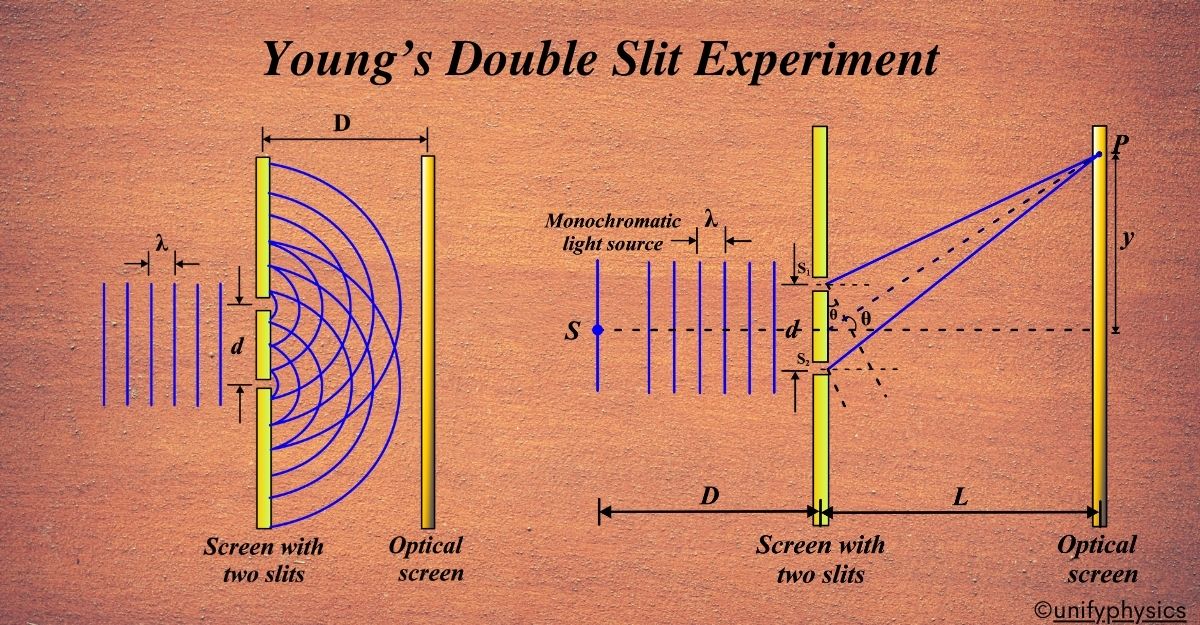
The story of Young’s Double Slit Experiment begins in the early 19th century with a physicist named Thomas Young. At that time, the nature of light was a hotly debated topic. Some scientists, like Isaac Newton, thought light was made up of particles, while others believed it behaved like a wave.
Imagine if light were like tiny balls thrown at a wall with two slits; you’d expect to see two bright spots directly behind the slits on a screen, right? That’s the particle theory. But what if light were more like ripples in a pond, spreading out and overlapping after passing through the slits? This is the wave theory, which suggests a pattern of several bright and dark bands due to the ripples interfering with each other.
In 1801, Thomas Young set out to settle this debate. He conducted an experiment where he shone light through two closely spaced slits onto a screen. Instead of just two bright spots, he observed a series of alternating bright and dark bands known as interference fringes. This pattern could only be explained if light behaved like waves, overlapping and combining to create the bands.
Young’s experiment was revolutionary because it provided strong evidence for the wave theory of light, which was initially proposed by Christiaan Huygens. It showed that light waves could interfere with each other, just like waves on water, creating patterns of constructive interference (bright bands) where the waves add up, and destructive interference (dark bands) where they cancel out.
Young’s Double Slit Experiment laid the foundation for the field of wave optics and was a precursor to the development of quantum mechanics. It also led to the understanding of the wave-particle duality of light, which is a fundamental concept in modern physics.
By conducting this simple yet ingenious experiment, Thomas Young not only advanced the wave theory of light but also set the stage for future discoveries that would transform our understanding of the universe.
Interference of Light Waves
Interference is a fundamental phenomenon observed when two or more waves overlap in space, resulting in a new wave pattern. This concept is crucial in understanding various optical effects and is particularly significant in the study of light waves.
When light waves from different sources meet, they don’t just pass by each other. Instead, they interact in such a way that they can add up to make a brighter light (constructive interference) or cancel each other out to create darkness (destructive interference). This interaction is what we call interference.
Coherent Light Sources: For interference to be observable, the light sources need to be coherent. This means they emit waves that have a constant phase difference and the same frequency. Without coherence, the interference pattern would be washed out and not visible.
Constructive Interference: This occurs when the crests (high points) of two waves align together, or the troughs (low points) align. The waves reinforce each other, making a wave that’s bigger than either of the individual waves. This results in a bright spot in the interference pattern.
Destructive Interference: In contrast, destructive interference happens when the crest of one wave meets the trough of another. They effectively cancel each other out, leading to a dark spot in the interference pattern.
Path Difference and Phase Difference: The reason why waves interfere is due to differences in the path they travel (path difference) or their phase (phase difference). When the path difference between two waves is an integer multiple of the wavelength, they are in phase and create constructive interference. When the path difference is a half-integer multiple of the wavelength, they are out of phase and create destructive interference.
Superposition Principle: The principle of superposition states that when two or more waves meet, the resultant wave is the sum of the individual waves. This principle is key to predicting the outcome of interfering light waves.
Understanding interference is essential for explaining many optical phenomena and technologies, such as holography, the iridescence of a soap bubble, and even the working of lasers. It’s a concept that shows the wave-like nature of light and helps us understand how light can behave in such complex and beautiful ways.
Young’s Double Slit Experiment
Young’s Double Slit Experiment (YDSE) is a classic physics experiment that demonstrates the wave nature of light. It’s named after Thomas Young, who first experimented in 1801 to prove that light can interfere with itself, much like waves do.
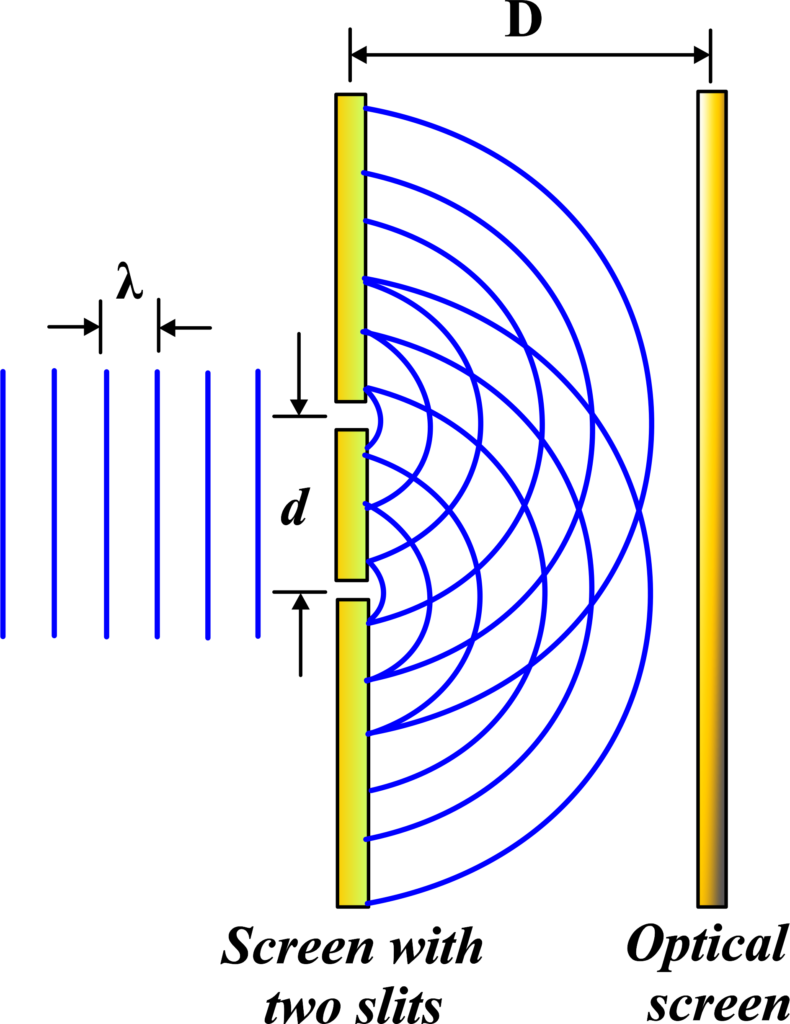
In YDSE, light from a single source is split into two separate waves by passing it through two closely spaced slits. When these two waves overlap on the other side, they create an interference pattern of bright and dark fringes on a screen placed behind the slits.
The bright fringes, or bands, occur where the waves from the two slits arrive in phase and reinforce each other, a phenomenon known as constructive interference. The dark fringes appear where the waves are out of phase and cancel each other, which is called destructive interference.
The pattern of fringes can be described mathematically. The equation gives the position of the bright fringes:
\(\displaystyle y_m = \frac{m\lambda D}{d} \)
where (ym) is the distance from the central fringe to the (m)-th bright fringe, (λ) is the wavelength of the light, (D) is the distance from the slits to the screen, (d) is the distance between the slits, and (m) is the order of the fringe.
YDSE is important because it provides direct evidence of the wave nature of light. Before this experiment, many scientists believed that light consisted of particles. The interference pattern observed in YDSE could not be explained by particle theory, thus supporting the wave theory of light.
Setup: The setup includes a light source, a screen, and a barrier with two closely spaced slits. The light source emits coherent light, which passes through the slits and forms an interference pattern on the screen.
The setup of Young’s Double Slit Experiment is elegantly simple. It consists of:
- A coherent light source, such as a laser, emits light of a single wavelength.
- A barrier with two very narrow, parallel slits separated by a small distance.
- A screen is positioned to capture the light after it passes through the slits.
The light source is placed in such a way that its rays fall directly on the barrier. The slits act as two new sources of light waves, which then spread out due to diffraction.
Working: As light waves pass through the slits, they spread out and overlap, creating regions of constructive interference (bright fringes) and destructive interference (dark fringes).
When the light waves emerging from the two slits meet, they interfere with each other. If the crests of the waves from both slits align, they create a bright spot on the screen due to constructive interference. If a crest from one slit meets a trough from the other, they cancel each other out, resulting in a dark spot due to destructive interference.
This interference pattern of alternating bright and dark fringes is projected onto the screen, demonstrating the wave nature of light. The central bright fringe, known as the central maximum, is the result of the direct overlap of light waves from both slits.
The experiment shows that light waves can be split and combined to form patterns, which is only possible if light behaves as a wave. This setup and the resulting pattern provide a clear demonstration of the fundamental principle of interference in wave optics.
Derivation for YDSE
In Young’s Double Slit Experiment, we use a monochromatic light source (S) placed far from two slits (S1) and (S2). This setup ensures that (S1) and (S2) act as coherent sources, emitting light waves with a constant phase difference. The light waves from these slits interfere with each other on a screen located at a distance (D) from the slits. The distance between two slits is denoted by the letter ‘d.’
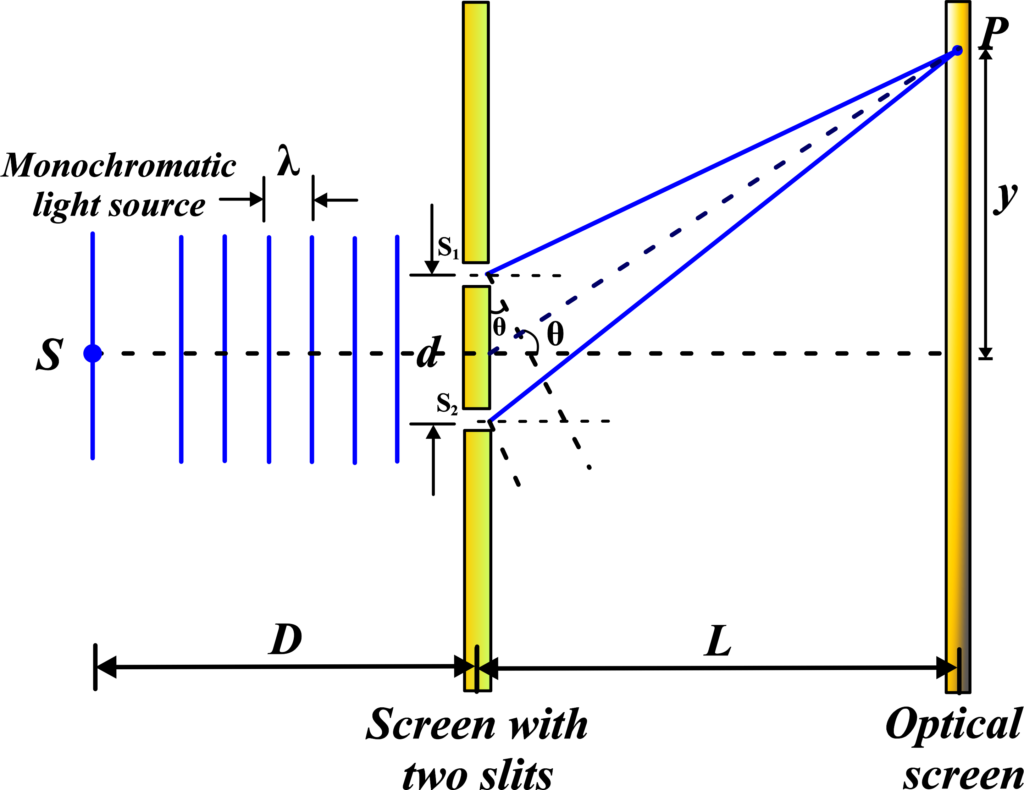
Path Difference: When light passes through slits (S1) and (S2) and reaches point ( P ) on the screen, it travels different distances from each slit. This difference in path length creates an interference pattern.
- Path Length from (S1) to (P): (S1P )
- Path Length from (S2) to (P): (S2P )
The path difference (∆) between these two paths is given by:
\(\displaystyle \Delta = S_2P – S_1P \)
For constructive interference (bright fringes), this path difference must be an integer multiple of the wavelength (λ):
\(\displaystyle \Delta = n\lambda \quad \text{(for } n = 0, 1, 2, \ldots) \)
For destructive interference (dark fringes), the path difference must be an odd multiple of half the wavelength:
\(\displaystyle \Delta = \left( n + \frac{1}{2} \right)\lambda \quad \text{(for } n = 0, 1, 2, \ldots) \)
Approximations in Young’s Double Slit Experiment:
Considering the geometry of the setup, if (d) is the distance between the slits and (D) is the distance from the slits to the screen, and assuming (D) is much larger than (d), the path difference (∆) can be approximated using the small-angle approximation.
Approximation 1: The path difference (∆) can be approximated as:
\(\displaystyle\Delta \approx d \sin \theta \)
Where (θ) is the angle that the line from the midpoint between the slits to point (P) makes with the perpendicular bisector of the line joining the slits.
Approximation 2: Using the small-angle approximation
(\(\displaystyle \sin \theta \approx \theta \approx \frac{y}{D} \)),
where ( y ) is the vertical displacement from the central point on the screen, we get:
\(\displaystyle \Delta \approx d \frac{y}{D} \)
Position of Fringes
(i) Bright Fringes: Bright fringes, or bright bands, appear on the screen at positions where light from both slits arrives in phase. This means the waves reinforce each other, creating a brighter image. Bright fringes occur where the path difference is an integer multiple of the wavelength.
Substituting the path difference for constructive interference:
\(\displaystyle d \frac{y}{D} = n\lambda \)
Solving for (y):
\(\displaystyle y = \frac{n\lambda D}{d} \)
This equation gives the positions (y) of the bright fringes on the screen.
(ii) Dark Fringes: Dark fringes, or dark bands, occur where light from the slits arrives out of phase, causing the waves to cancel each other out.
For destructive interference, the path difference is:
\(\displaystyle d \frac{y}{D} = \left( n + \frac{1}{2} \right) \lambda \)
Solving for (y)
\(\displaystyle y = \left( n + \frac{1}{2} \right) \frac{\lambda D}{d} \)
This equation gives the positions (y) of the dark fringes on the screen.
(iii) Fringe Width: The fringe width (β) is the distance between two successive bright or dark fringes on the screen. For constructive interference (bright fringes), the position of the (n)-th bright fringe is given by:
\(\displaystyle y_n = \frac{n \lambda D}{d} \)
For the (n+1)-th bright fringe:
\(\displaystyle y_{n+1} = \frac{(n+1) \lambda D}{d} \)
The fringe width (β) is the distance between these two fringes:
\(\displaystyle \beta = y_{n+1} – y_n \)
\(\displaystyle \beta = \frac{(n+1) \lambda D}{d} – \frac{n \lambda D}{d} \)
\(\displaystyle \beta = \frac{\lambda D}{d} \)
Thus, the fringe width is:
\(\displaystyle \beta = \frac{\lambda D}{d} \)
(iv) Angular Width: The angular width (θ) of a fringe is the angle subtended by the fringe width at the slits.
Since the fringe width is (β) and the distance to the screen is (D), the angular width (∆θ) is:
\(\displaystyle \Delta \theta = \frac{\beta}{D} \)
Substitute the fringe width ( \(\displaystyle\beta = \frac{\lambda D}{d} \)):
\(\displaystyle \Delta \theta = \frac{\frac{\lambda D}{d}}{D}\)
\(\displaystyle \Delta \theta = \frac{\lambda}{d} \)
Thus, the angular width of a fringe is:
\(\displaystyle \Delta \theta = \frac{\lambda}{d} \)
(v) Maximum Order: The maximum order of interference fringes is limited by the wavelength and slit separation.
The maximum order (nmax) of the fringe is the highest order bright fringe that can be observed on the screen. For constructive interference, the path difference should be an integer multiple of the wavelength:
\(\displaystyle d \sin \theta = n \lambda \)
The maximum value of ( \(\displaystyle\sin \theta \)) is 1, so:
\(\displaystyle d = n_{\text{max}} \lambda \)
Thus, the maximum order ( \(\displaystyle n_{\text{max}} \)) is:
\(\displaystyle n_{\text{max}} = \frac{d}{\lambda} \)
These expressions help in understanding the spacing and angular spread of the fringes, as well as the maximum number of observable fringes in Young’s Double Slit Experiment.
Shape of Interference Fringes
The fringes are typically hyperbolic but appear straight and parallel due to the large distance between the screen and the slits. In Young’s Double Slit Experiment, the interference pattern that appears on the screen consists of a series of bright and dark bands known as interference fringes. These fringes are the result of constructive and destructive interference between light waves coming from the two slits.
Hyperbolic Nature: The actual shape of these fringes is hyperbolic. This means that if you were to trace the path of the bright and dark bands, they would form hyperbolas. However, because the screen is usually placed far away from the slits (the distance (D) is much larger than the slit separation (d), the fringes appear to be straight and parallel lines.
Why They Appear Straight: The reason the fringes look straight is due to the angles involved. When the screen is far away, the angles at which the light from the two slits meet are very small. This makes the curves of the hyperbolas so gentle that they look like straight lines to the naked eye.
Also Read: Coherent And Incoherent Addition of Waves
Intensity of Fringes
(i) Maximum Intensity: In Young’s Double Slit Experiment, the maximum intensity of fringes refers to the brightest points in the interference pattern.
- The maximum intensity of the fringes occurs at points where the light waves from both slits constructively interfere. This means that the crests of the waves from both slits align perfectly, reinforcing each other and resulting in a bright fringe.
- The central fringe, or the central maximum, is typically the brightest because it is the point of perfect constructive interference, where the path difference between the two waves is zero.
The intensity (I) of the bright fringes can be mathematically represented as proportional to the square of the amplitude of the resultant wave. If (A) is the amplitude of the individual waves, then the intensity at the central maximum is given by:
\(\displaystyle I_{max} = 4A^2 \)
This is because, at the central maximum, the amplitudes of the waves from both slits add up coherently (A + A = 2A), and since intensity is proportional to the square of the amplitude, the intensity becomes (2A)2 = 4A2 ).
The concept of maximum intensity is crucial for students to understand because it illustrates the energy distribution across the interference pattern. It shows how the wave nature of light can lead to regions of high energy (brightness) due to the constructive superposition of waves.
(ii) Minimum Intensity: In the context of Young’s Double Slit Experiment, the minimum intensity of fringes refers to the darkest points on the interference pattern.
- The minimum intensity occurs at points of destructive interference, where the waves from the two slits are out of phase.
- At these points, the crest of one wave meets the trough of another, leading to cancellation. The amplitude of the resultant wave is minimized, resulting in a dark fringe.
If the individual waves have an amplitude (A), the amplitude of the resultant wave at the points of destructive interference is (A – A = 0).
Since the intensity of light is proportional to the square of the amplitude, the intensity at these points is (Imin = (0)2 = 0 ).
Practically, due to imperfections in the setup or the quality of the light source, the intensity may not be exactly zero but is significantly lower than that of the bright fringes. These dark fringes are equally spaced between the bright fringes and provide contrast to the pattern, making the bright fringes more noticeable.
Special Cases
(i) Rays Not Parallel to Principal Axis
In Young’s Double Slit Experiment, we usually assume that the light rays coming from the slits to any point on the screen are parallel. This assumption simplifies the analysis and is valid when the screen is far away from the slits. However, there are special cases where this assumption does not hold, particularly when the rays are not parallel.
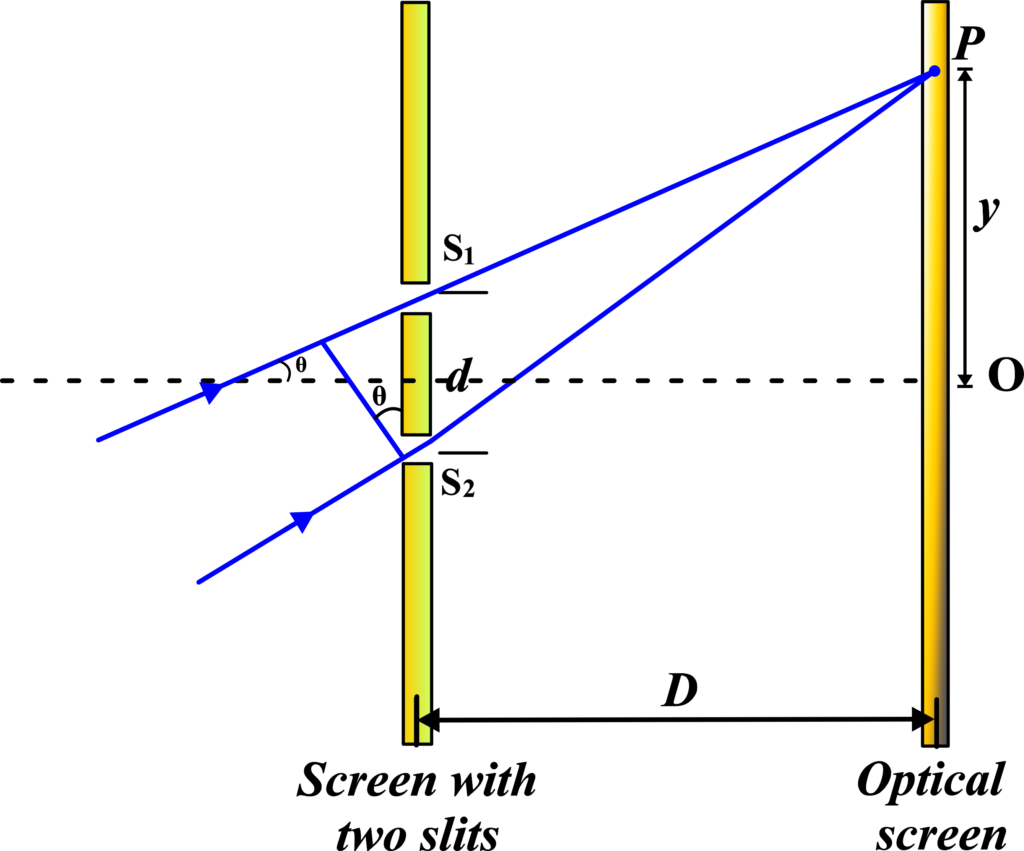
When the rays from the slits are not parallel, it means they are converging or diverging as they travel toward the screen. This can happen if the light source is not placed far enough from the slits or if the slits themselves are not aligned properly.
Non-parallel rays can cause the interference pattern to shift or distort. Instead of a symmetrical pattern centered on the normal (the line perpendicular to the screen and passing through the midpoint between the slits), the fringes may be skewed or displaced.
To understand this concept, imagine the light waves as water ripples in a pond. If you drop two stones at different distances from the shore, the ripples won’t meet at the same angle along the entire shoreline. Similarly, if the light waves from the slits are not parallel, they will interfere at different angles, affecting the symmetry of the fringe pattern.
When rays are not parallel to the principal axis, we need to consider the angle at which the light source is positioned relative to the central line between the two slits.
When rays are not parallel to the principal axis, the path difference calculation changes due to the different angles of incidence.
- (θ) is the angle of incidence.
- (∆x ) is the path difference.
Path Difference:
\(\displaystyle\Delta x = (AS_1 + S_1P) – S_2P\)
From the geometry:
\(\displaystyle\Delta x = AS_1 – (S_2P – S_1P)\)
\(\displaystyle\Delta x = d \sin \theta – \frac{4d}{D}y\)
Condition for Maxima and Minima:
For maxima:
\(\displaystyle\Delta x = n\lambda\)
For minima:
\(\displaystyle\Delta x = (2n – 1) \frac{\lambda}{2}\)
Using these equations, we can calculate different positions of maxima and minima.
(ii) Source Placed Beyond the Central Line
In Young’s Double Slit Experiment, a special case arises when the light source is placed beyond the central line that bisects the distance between the two slits. Typically, the light source in Young’s Double Slit Experiment is aligned such that it is equidistant from both slits. This ensures that the light waves originating from the slits have symmetrical paths to any point on the screen, resulting in a symmetrical interference pattern.
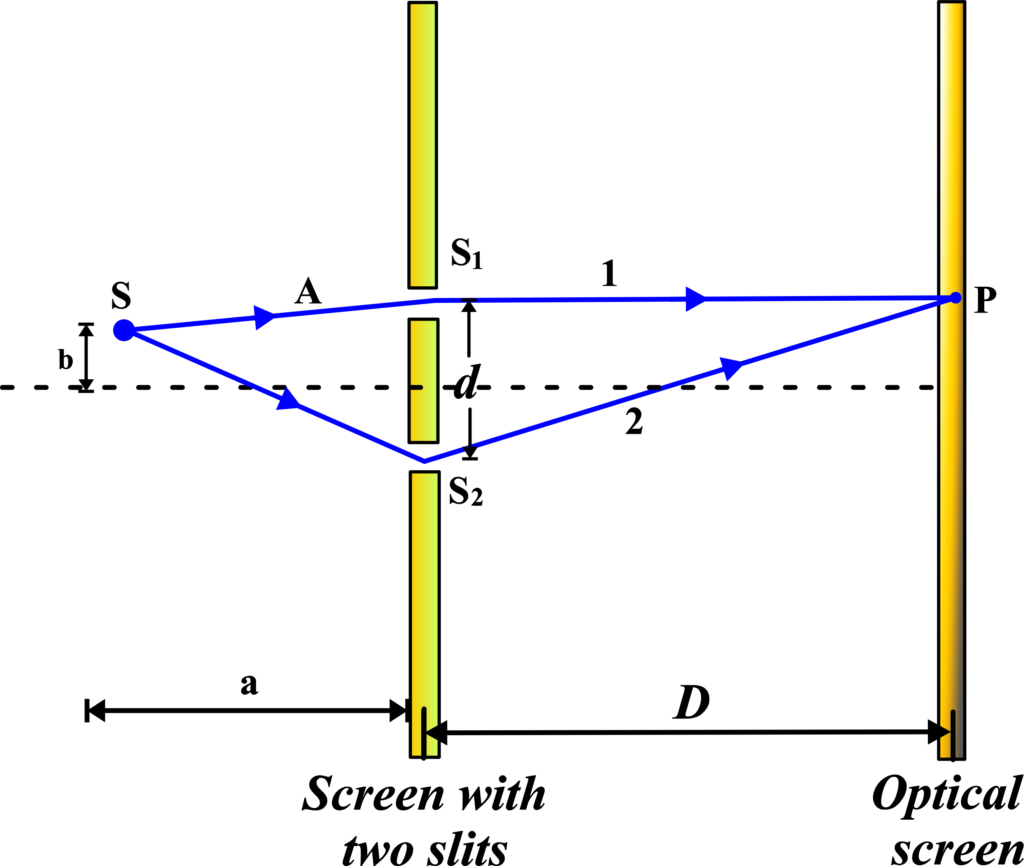
If the source is placed beyond the central line, the symmetry is broken. One slit is now closer to the source than the other. This means that the light waves from the closer slit will have a shorter path to travel to reach any point on the screen compared to waves from the farther slit.
When the source is placed above or below the central line, the path difference calculation changes due to the different distances to the slits.
- (S1) and (S2) are the slits.
- (P) is a point on the screen.
- (d) is the distance between the slits.
- (D) is the distance from the slits to the screen.
- (a) is the horizontal distance between the source and the central line.
- (b) is the vertical distance between the source and the slits.
- (Δx) is the path difference.
Path Difference:
\(\displaystyle\Delta x = (\text{distance of ray 2}) – (\text{distance of ray 1})\)
From the geometry:
\(\displaystyle\Delta x = (S_2P + S_2P) – (S_1S + S_1P)\)
\(\displaystyle\Delta x = (S_2P + S_1) – (S_2P – S_1P)\)
\(\displaystyle\Delta x = \frac{bd}{a} + \frac{yd}{D}\)
Condition for Maxima and Minima:
For maxima:
\(\displaystyle\Delta x = n\lambda\)
For minima:
\(\displaystyle\Delta x = (2n – 1) \frac{\lambda}{2}\)
By knowing the value of (∆x ) from the above expressions, we can calculate different positions of maxima and minima.
The result is a shift in the interference pattern. The central maximum may no longer be directly in front of the midpoint between the two slits. Instead, it shifts towards the slit closer to the source. The entire pattern of bright and dark fringes will also shift accordingly, and the fringes may no longer be evenly spaced across the screen.
This shift can be understood by considering the path difference between the waves from the two slits. Since the path difference changes due to the off-center placement of the source, the conditions for constructive and destructive interference at various points on the screen also change.
Displacement of Fringes
In Young’s Double Slit Experiment, the displacement of fringes refers to the shift in the position of the bright and dark bands on the screen due to changes in the experimental setup or external conditions.
Causes of Displacement:
- Change in Wavelength: If the wavelength of light used in the experiment changes, the fringe pattern will shift. A longer wavelength will cause the fringes to move further apart, while a shorter wavelength will bring them closer together.
- Change in Medium: Introducing a different medium (like water or glass) into the path of one of the beams can alter the speed of light in that path, leading to a shift in the interference pattern.
- Movement of the Screen or Slits: Physically moving the screen or the slits closer or further away from each other can also cause the fringes to shift.
The displacement can be quantified by measuring the change in position of the central bright fringe or any other fringe. This shift is directly related to the path difference between the light waves from the two slits.
When a thin transparent plate of thickness (t) is introduced in front of one of the slits in Young’s double-slit experiment, the fringe pattern shifts toward the side where the plate is present. This is due to the change in optical path length caused by the introduction of the plate. Let’s derive the expression for the displacement of fringes.
- (S1) and (S2) are the slits separated by distance (d).
- (P) and (P1) are points on the screen where fringes are observed.
- ( S ) is a point on the screen where a fringe is observed without the plate.
- A transparent plate of thickness (t) and refractive index (µ) is placed in front of slit (S2).
Path Difference Before Introducing the Plate
Without the Plate: The path difference between the light rays from (S1) and (S2) at point (P) is:
\(\displaystyle\delta = S_1P – S_2P\)
Path Difference After Introducing the Plate
With the Plate:
The path length for the light ray passing through (S2) changes due to the plate. The new optical path length for the light from (S2) is:
\(\displaystyle S_2P_1 = (S_2P_1 – t){\text{air}} + t{\text{plate}} = (S_2P_1 – t) + \mu t\)
Simplifying this, we get:
\(\displaystyle S_2P_1 = S_2P_1 + (\mu – 1)t\)
New Path Difference:
The new path difference between the light rays from (S1) and (S2) at point (P1) is:
\(\displaystyle(\delta){\text{new}} = S_1P_1 – S_2P_1 = S_1P_1 – (S_2P_1 + (\mu – 1)t) \)
\(\displaystyle (\delta x){\text{new}} = (S_1P_1 – S_2P_1) – (\mu – 1)t\)
Using the original path difference ( \(\displaystyle\delta x = d \sin \theta\) ):
\(\displaystyle (\delta x)_{\text{new}} = d \sin \theta – (\mu – 1)t\)
Fringe Shift Calculation
Fringe Position: The position of fringes is given by:
\(\displaystyle y = \frac{\delta x D}{d}\)
For the new path difference:
\(\displaystyle y_{\text{new}} = \frac{(\Delta x)_{\text{new}} D}{d}\)
\(\displaystyle = \frac{(d \sin \theta – (\mu – 1)t) D}{d}\)
Simplifying, we get:
\(\displaystyle y_{\text{new}} = \frac{d \sin \theta D}{d} – \frac{(\mu – 1)t D}{d}\)
\(\displaystyle y_{\text{new}} = D \sin \theta – \frac{(\mu – 1)t D}{d}\)
Fringe Displacement: The displacement of the fringes (\(\displaystyle \delta y\)) is the difference between the new and the original fringe positions:
\(\displaystyle\delta y = y_{\text{new}} – y\)
\(\displaystyle\delta y = \left( D \sin \theta – \frac{(\mu – 1)t D}{d} \right) – D \sin \theta\)
\(\displaystyle\delta y = – \frac{(\mu – 1)t D}{d}\)
Thus, the expression for the displacement of fringes in Young’s double-slit experiment when a thin transparent plate is introduced is:
\(\displaystyle \delta y = – \frac{(\mu – 1)t D}{d} \)
This shows that the fringe pattern shifts towards the side where the plate is present by an amount (\(\displaystyle\frac{(\mu – 1)t D}{d}\)).
Constructive and Destructive Interference
Constructive Interference:
What is Constructive Interference?– Constructive interference occurs when two or more waves meet and their displacements are in the same direction. This means that the crests (the highest points) of one wave align with the crests of another wave, and the troughs (the lowest points) align as well.
When waves interfere constructively, their amplitudes add together. The amplitude is the height of the wave from the center line to the crest. So, if two waves with the same amplitude interfere constructively, the resultant wave will have an amplitude that is double the individual waves’ amplitudes.
For constructive interference to occur, the waves must have a phase difference that is an even multiple of π (180°). This means the waves are ‘in phase’ and their peaks and troughs match up perfectly as they combine.
Imagine two ripples in a pond that are heading towards each other. If they meet and the peak of one ripple meets the peak of the other, they will combine to create a higher ripple. This is constructive interference in action.
Destructive Interference:
Occurs when the crest of one wave aligns with the trough of another, resulting in darkness or cancellation. When two waves of the same frequency and wavelength meet, if the crest of one wave aligns with the trough of another, they interfere destructively. This happens because the high point of one wave fills in the low point of the other, resulting in a wave with a reduced (or zero) amplitude.
The waves must be out of phase by an odd multiple of half the wavelength, which means the path difference between them is
\(\displaystyle (2n-1)\frac{\lambda}{2} \),
where (n) is an integer, and (λ) is the wavelength.
The phase difference between the waves should be (\(\displaystyle (2n-1)\pi \)), indicating that they are half a cycle out of sync.
The amplitude of the resulting wave at points of destructive interference is significantly lower than the individual waves. If the waves have equal amplitude, the resulting amplitude can be zero, leading to a point of no wave movement, known as a node.
Sample Questions
Problem: Derive the expression for the fringe spacing (fringe width) in Young’s Double Slit Experiment.
Solution: In YDSE, light from a coherent source is split into two waves by two slits, (S1) and (S2), separated by a distance (d). These waves interfere with a screen placed at a distance (D) from the slits.
Path Difference: The path difference (∆x ) between the two waves arriving at a point (P) on the screen is given by:
\(\displaystyle\Delta x = d \sin \theta\)
For small angles, ( \(\displaystyle\sin \theta \approx \tan \theta = \frac{y}{D} \)), where (y) is the distance from the central maximum to point (P):
\(\displaystyle\Delta x = d \frac{y}{D}\)
Constructive Interference: For constructive interference (bright fringes), the path difference must be an integer multiple of the wavelength (λ):
\(\displaystyle d \frac{y_n}{D} = n\lambda \quad \Rightarrow \quad y_n = \frac{n\lambda D}{d}\)
Fringe Spacing: The fringe spacing (or fringe width) (β) is the distance between two successive bright fringes:
\(\displaystyle\beta = y_{n+1} – y_n = \frac{(n+1)\lambda D}{d} – \frac{n\lambda D}{d} = \frac{\lambda D}{d}\)
The fringe spacing (fringe width) in Young’s Double Slit Experiment is given by (\(\displaystyle \beta = \frac{\lambda D}{d}\) ).
Problem: Derive the expression for the intensity at any point on the screen in Young’s Double Slit Experiment.
Solution: The intensity at a point on the screen in YDSE depends on the superposition of the light waves from the two slits.
Electric Fields: Let the electric fields due to the slits (S1) and (S2) be (E1) and (E2), respectively. Assuming equal amplitudes (E0):
\(\displaystyle E_1 = E_0 \cos (\omega t)\)
\(\displaystyle E_2 = E_0 \cos (\omega t + \phi)\)
where (\(\displaystyle \phi \)) is the phase difference due to the path difference (∆x).
Resultant Electric Field: The resultant electric field (E) is:
\(\displaystyle E = E_1 + E_2 = E_0 \cos (\omega t) + E_0 \cos (\omega t + \phi)\)
Using the trigonometric identity for the sum of cosines:
\(\displaystyle E = 2E_0 \cos \left( \frac{\phi}{2} \right) \cos \left( \omega t + \frac{\phi}{2} \right)\)
Intensity: The intensity (I) is proportional to the square of the amplitude of the resultant electric field:
\(\displaystyle I = E^2 \propto \left[ 2E_0 \cos \left( \frac{\phi}{2} \right) \right]^2 = 4E_0^2 \cos^2 \left( \frac{\phi}{2} \right)\)
Let (I0) be the intensity due to one slit. Therefore, the total intensity (I) is:
\(\displaystyle I = 4I_0 \cos^2 \left( \frac{\phi}{2} \right)\)
Phase Difference: The phase difference (\(\displaystyle \phi\) ) is related to the path difference (∆x) by (\(\displaystyle \phi = \frac{2\pi}{\lambda} \Delta x\) ). For small angles, (\(\displaystyle\Delta x = d \sin \theta \approx d \frac{y}{D}\)):
\(\displaystyle\phi = \frac{2\pi}{\lambda} d \frac{y}{D}\)
Thus, the intensity at a point (y) on the screen is:
\(\displaystyle I = 4I_0 \cos^2 \left( \frac{\pi d y}{\lambda D} \right)\)
The intensity at a point (y) on the screen in Young’s Double Slit Experiment is given by (\(\displaystyle I = 4I_0 \cos^2 \left( \frac{\pi d y}{\lambda D} \right) \)), where (I0) is the intensity due to one slit.
Problem: Calculate the position of the third bright fringe on a screen 2 m away from the slits in Young’s Double Slit Experiment, given (d = 0.1) mm and (λ = 600) nm.
Solution: The position of the ( n )-th bright fringe is given by:
\(\displaystyle y_n = \frac{n\lambda D}{d}\)
For the third bright fringe (n = 3):
\(\displaystyle y_3 = \frac{3 \times 600 \times 10^{-9} \times 2}{0.1 \times 10^{-3}}\)
Calculate:
\(\displaystyle y_3 = \frac{3 \times 600 \times 10^{-9} \times 2}{0.1 \times 10^{-3}} = \frac{3 \times 600 \times 2}{0.1} \times 10^{-6} \)
\(\displaystyle = \frac{3600}{0.1} \times 10^{-6} = 36000 \times 10^{-6} = 0.036 \text{ m}\)
The position of the third bright fringe is 0.036 m (36 mm) from the central maximum.
Problem: A glass plate of thickness 0.5 mm and refractive index 1.5 is introduced in the path of one of the beams in Young’s Double Slit Experiment. Calculate the shift in the central fringe.
Solution: The introduction of a glass plate changes the optical path length of the beam passing through it. The optical path length change (∆L) is given by:
\(\displaystyle\Delta L = (n – 1)t\)
Substitute the given values:
\(\displaystyle\Delta L = (1.5 – 1) \times 0.5 \times 10^{-3} = 0.5 \times 0.5 \times 10^{-3} = 0.25 \times 10^{-3} \text{ m} = 250 \text{ nm}\)
The path difference (∆x ) introduced by the plate causes a shift in the fringe pattern. The fringe shift (∆y ) can be calculated using the fringe spacing formula:
\(\displaystyle\Delta y = \frac{\Delta L \cdot D}{d}\)
Assuming (D = 2 m) and (d = 0.1 mm = 0.1 × 10-3 m):
\(\displaystyle\Delta y = \frac{250 \times 10^{-9} \times 2}{0.1 \times 10^{-3}} = \frac{250 \times 2}{0.1} \times 10^{-6} \)
\(\displaystyle = \frac{500}{0.1} \times 10^{-6} = 5000 \times 10^{-6} = 0.005 \text{ m} = 5 \text{ mm}\)
The introduction of a glass plate of thickness 0.5 mm and refractive index 1.5 in the path of one of the beams in YDSE causes the central fringe to shift by 5 mm.
FAQs
What is Young’s Double Slit Experiment (YDSE) and why is it significant?
Young’s Double Slit Experiment is a foundational experiment in physics that demonstrates the wave nature of light. By allowing light to pass through two closely spaced slits and observing the resulting interference pattern on a screen, the experiment provides evidence for the principle of superposition and the wave behavior of light. It is significant because it challenged the classical particle view of light and supported the wave theory.
What is the basic derivation for the fringe pattern in YDSE?
The basic derivation for the fringe pattern in YDSE involves considering the path difference between light waves coming from the two slits to a point on the screen. This path difference leads to constructive or destructive interference, creating bright and dark fringes. The positions of these fringes can be derived by analyzing the geometry of the setup and applying the principle of superposition.
What approximations are commonly used in Young’s Double Slit Experiment?
Common approximations in YDSE include assuming the screen is far from the slits (far-field approximation) so that the light rays are nearly parallel, and considering the slit separation to be much smaller than the distance to the screen. These approximations simplify the calculations and allow for the use of linear approximations for the path difference.
How is the position of the fringes determined in YDSE?
The position of the fringes in YDSE is determined by the condition for constructive and destructive interference. For constructive interference (bright fringes), the path difference between the waves from the two slits must be an integer multiple of the wavelength. For destructive interference (dark fringes), the path difference must be an odd multiple of half wavelengths. These conditions give the positions of the bright and dark fringes on the screen.
How is the intensity of fringes calculated in YDSE?
The intensity of fringes in YDSE is calculated based on the principle of superposition of the electric fields from the two slits. Constructive interference results in maximum intensity, while destructive interference results in minimum (or zero) intensity. The intensity pattern follows a cosine-squared distribution for constructive and destructive interference points.
What happens if the rays in YDSE are not parallel?
If the rays in YDSE are not parallel, the interference pattern can become distorted. The assumption of parallel rays is an approximation that simplifies the analysis. In reality, if the rays diverge or converge, the fringe spacing may change, and the fringes may not be perfectly straight or evenly spaced. This deviation can be accounted for with more complex calculations that do not assume parallel rays.
How does placing the source beyond the central line affect the fringe pattern and what is fringe displacement?
Placing the source beyond the central line in YDSE causes the entire fringe pattern to shift sideways. This shift is known as fringe displacement. The central maximum (the bright fringe at the center) moves from the geometric center of the screen to a new position corresponding to the new optical path difference. This displacement can be calculated and is used in various applications to measure small changes in optical path lengths or displacements.