The story of potential energy begins with the ancient Greeks, particularly with Aristotle’s concept of “potentiality.” Aristotle observed that objects have the potential to change states, such as a rock on a hill that can roll down.
Fast forward to the 17th century, and we see the concept of potential energy taking a more scientific form. Scientists like Galileo Galilei and Sir Isaac Newton began to describe how objects at rest could have energy due to their position.
However, the term “potential energy” was not coined until the 19th century by William Rankine, a Scottish engineer and physicist. Rankine introduced the term to describe the energy that is stored within an object and can be released to do work.
Rankine’s work helped to formalize the idea that energy is not just something that happens when objects move (kinetic energy), but also something that exists in the potential for movement. This was a significant leap in understanding energy, as it allowed scientists to calculate the energy in systems even when they weren’t moving.
What is Potential Energy?
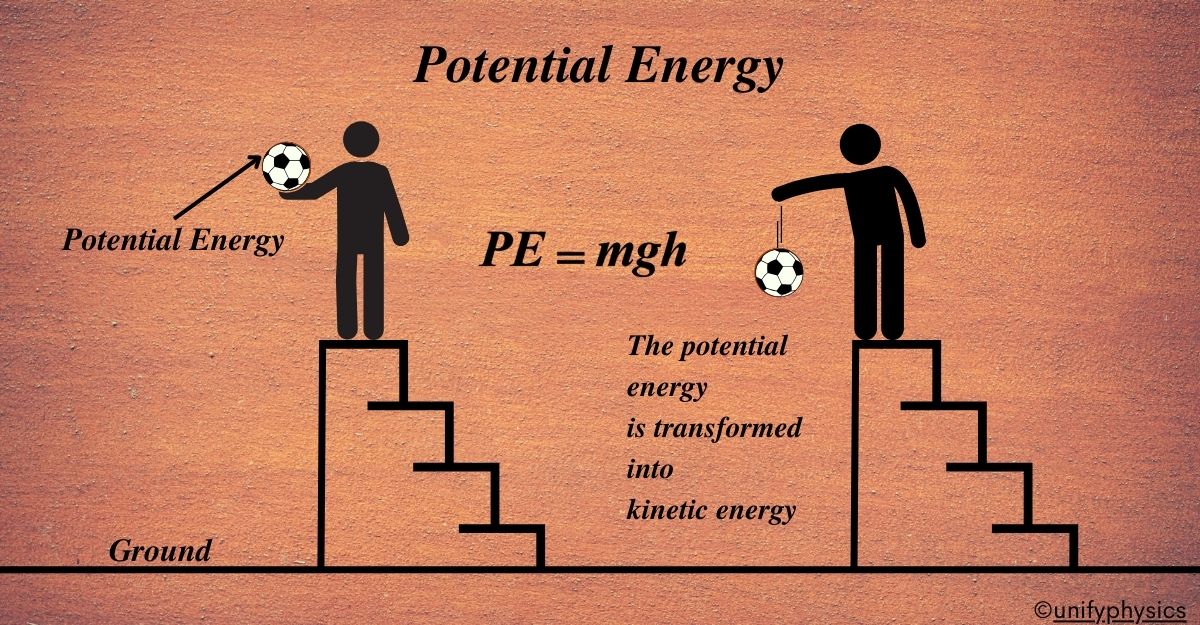
Potential Energy (PE) is the energy stored in an object due to its position, condition, or configuration. It’s like the energy waiting to be released when the object’s position or condition changes.
Potential energy is a form of energy that an object possesses due to its position or configuration within a system, or due to the forces acting on it. It is energy that is stored and can be converted into other forms of energy, such as kinetic energy, when the object’s position or configuration changes.
Potential energy arises from the idea that certain positions or configurations of objects within a system are associated with stored energy. This stored energy represents the potential for the object to do work or to undergo changes in its motion or state when acted upon by external forces.
In simpler terms, think of potential energy as the energy that an object has because of where it is or how it is arranged within a system. This energy can be thought of as “potential” because it can be converted into other forms of energy and produce effects such as motion or changes in the system. Understanding potential energy helps us comprehend how energy is stored and transformed within physical systems.
Imagine you’re at the top of a slide in a playground. You’re sitting there, not moving, but you can feel the anticipation of the slide down. That feeling is a lot like potential energy. It’s the energy that you have because of where you are, which in physics, we call your position.
Potential energy is the energy that an object has because of its position or state. It’s like a storage room of energy, waiting to be used. This energy comes from the work done to put the object in a particular position or state. For example, when you lift a book off the floor and place it on a shelf, you’re giving it potential energy because of its new position above the ground.
The formula for potential energy depends on the force acting on the object. For gravity, which is what pulls you down the slide, the formula is:
\(\displaystyle PE = m \times g \times h \)
- (m) is the mass of the object (how heavy it is)
- (g) is the acceleration due to gravity (the pull of Earth’s gravity)
- (h) is the height above the ground (how high the object is)
Potential Energy Unit: The unit for potential energy is the joule (J). It’s like the currency for energy; just as you use money to buy things, you use joules to measure energy.
Types of Potential Energy
Potential energy is a fundamental form of energy, constituting one of the two primary categories of energy. Within this classification, two main types of potential energy are recognized:
Gravitational Potential Energy
This is the energy an object possesses due to its position in a gravitational field. The higher the object is placed, the more gravitational potential energy it has.
Gravitational Potential Energy is like the energy of possibility. It’s the energy that an object has because of where it is on the Earth or another massive body. Think of it as the energy that an object has stored up, just waiting for the chance to move.
Imagine you’re holding a ball in your hand. The ball isn’t moving, but it has the potential to fall to the ground. That’s because Earth’s gravity is pulling on it. The energy that the ball has, because it’s in a high position, is what we call Gravitational Potential Energy.

The higher you lift the ball, the more gravitational potential energy it has. This is because you’re doing work against Earth’s gravity to lift the ball. The work you’ve done is stored as energy in the ball. If you let go of the ball, the stored energy is converted into kinetic energy as the ball falls.
The formula for Gravitational Potential Energy is pretty straightforward:
\(\displaystyle GPE = m \times g \times h \)
Example: Let’s say you lift a 1 kg textbook to a shelf that’s 2 meters high. The gravitational potential energy of the textbook is:
\(\displaystyle GPE = 1 \, \text{kg} \times 9.8 \, \text{m/s}^2 \times 2 \, \text{m} = 19.6 \, \text{J} \)
This means the textbook has 19.6 joules of energy stored in it because of its position. If the shelf breaks and the book falls, that energy will be released as the book moves.
Elastic Potential Energy
Let’s talk about Elastic Potential Energy (EPE), a concept that’s as stretchy as a rubber band and as compressible as a spring mattress. It’s a type of potential energy that’s all about flexibility and bounce-back.
Elastic potential energy is a type of potential energy associated with the deformation or compression of elastic materials, such as springs, rubber bands, or elastic cords. It arises due to the ability of these materials to store energy when they are stretched, compressed, or twisted away from their natural or equilibrium positions.
Consider a weight attached to a spring, suspended vertically from a support. When the weight is at rest, hanging motionless, it possesses potential energy due to its position in relation to the spring’s equilibrium position. This potential energy is termed elastic potential energy.
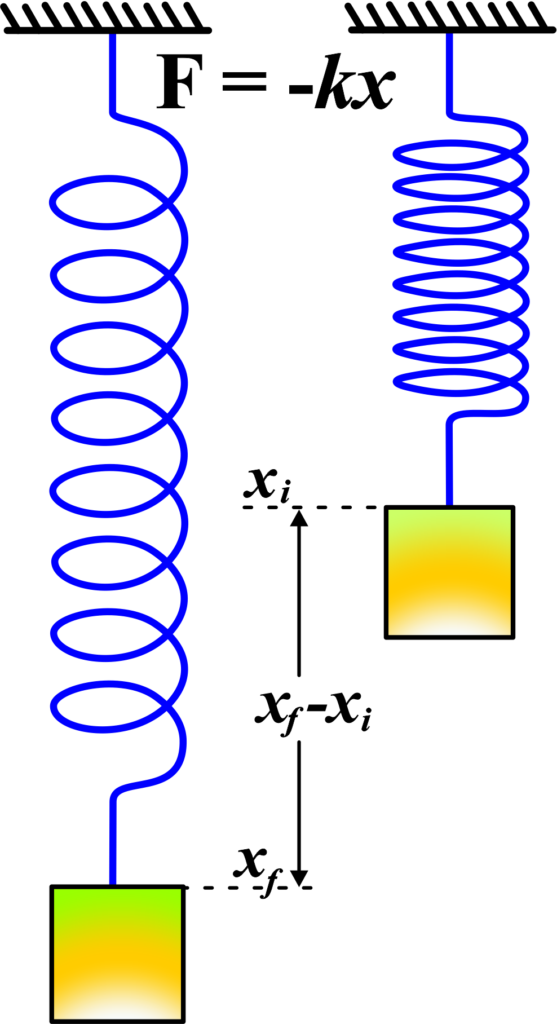
The spring, in its natural or equilibrium state, is neither stretched nor compressed. However, when a force (the weight of the object) is applied, causing the spring to stretch or compress, the spring stores energy. This stored energy is in the form of elastic potential energy.
As the weight is lifted or lowered, work is done against the restoring force of the spring, resulting in the deformation of the spring from its equilibrium position. The more the spring is stretched or compressed, the more elastic potential energy it stores.
When the weight is released, the spring exerts a force in the opposite direction to return to its equilibrium position. This force causes the weight to oscillate up and down. During this motion, the potential energy stored in the spring is converted into kinetic energy and back again, as the weight alternately speeds up and slows down.
Elastic potential energy can be understood as the energy stored within an elastic material when it is deformed from its original shape. When a force is applied to stretch or compress an elastic material, work is done on the material, and this work is stored as potential energy within the material.
When you stretch a rubber band, you’re doing work on it. You’re pulling it away from its relaxed state, and as you do this, you’re storing energy in it. This stored energy is what we call EPE. The same goes for compressing a spring in a toy car; when you let go, the spring snaps back, and the car zooms off. That’s EPE turning into kinetic energy.
The formula for Elastic Potential Energy is a bit different from gravitational potential energy. It’s based on how much you stretch or compress something and how stiff that something is. Here’s the formula:
\(\displaystyle EPE = \frac{1}{2} k x^2 \)
- (k) is the spring constant, which tells you how stiff the object is. The stiffer the object, the bigger the (k).
- (x) is the displacement from the object’s original, relaxed position. It’s how much you’ve stretched or compressed it.
Example: Imagine you have a spring with a spring constant ( k ) of 400 N/m, and you compress it by 0.1 meters (10 cm). The elastic potential energy stored in the spring would be:
\(\displaystyle EPE = \frac{1}{2} \times 400 \, \text{N/m} \times (0.1 \, \text{m})^2 \)
\(\displaystyle EPE = \frac{1}{2} \times 400 \, \text{N/m} \times 0.01 \, \text{m}^2 \)
\(\displaystyle EPE = 2 \, \text{J} \)
So, the spring has 2 joules of energy ready to be released when you let go.
Elastic Potential Energy is super important because it’s everywhere. It’s in the shoes that cushion your feet when you run, in the trampolines that send you flying, and even in the bridges that flex under the weight of cars but don’t break.
Also Read: Work-Energy Theorem
Difference Between Potential and Kinetic Energy
Potential Energy is the stored energy in an object due to its position or state. It is not relative to the environment of the object. Kinetic Energy is the energy of motion, possessed by an object due to its movement. It is relative to the state of other objects in its environment.
| Aspect | Potential Energy | Kinetic Energy |
|---|---|---|
| Definition | Energy that an object has due to its position or state. | Energy that an object possesses due to its motion. |
| Dependence | Depends on the object’s position relative to a reference point. | Depends on the object’s mass and velocity. |
| Formula | \(\displaystyle PE = m \times g \times h \) | \(\displaystyle KE = \frac{1}{2} m \times v^2 \) |
| Unit | Measured in joules (J). | Measured in joules (J). |
| Transferability | Not easily transferable. | Can be transferred from one object to another. |
| Relative | Non-relative to the environment of the object. | Relative to the environment of the object. |
| Examples | A book on a shelf, water behind a dam. | A rolling ball, a flying arrow. |
This table summarizes the key points that differentiate Potential Energy from Kinetic Energy. Potential Energy is like the energy stored in a bank, while Kinetic Energy is like the money being spent. Both are forms of energy, but they manifest in different ways depending on the state and movement of the object.
Solved Examples
Example 1: A mass of 2 kg is lifted to a height of 5 meters above the ground. Calculate its gravitational potential energy.
Solution : Given; Mass, (m = 2) kg ; Height, (h = 5) m ; Acceleration due to gravity, (g = 9.8 m/s2)
Gravitational Potential Energy (U) is given by:
\(\displaystyle U = mgh \)
Substituting the given values:
\(\displaystyle U = 2 \times 9.8 \times 5 = 98 \, \text{J} \)
Therefore, the gravitational potential energy is (98 J).
Example 2: A spring with a spring constant of (500 N/m) is compressed by (0.2 m). Calculate the elastic potential energy stored in the spring.
Solution: Given; Spring constant, (k = 500 N/m) ; Displacement, (x = 0.2 m)
Elastic Potential Energy (U) stored in the spring is given by:
\(\displaystyle U = \frac{1}{2} k x^2 \)
Substituting the given values:
\(\displaystyle U = \frac{1}{2} \times 500 \times (0.2)^2 \)
\(\displaystyle U = \frac{1}{2} \times 500 \times 0.04 \)
\(\displaystyle U = 10 \, \text{J} \)
Therefore, the elastic potential energy stored in the spring is (10 J).
Example 3: A block of mass (4 kg) is dropped from a height of (10 m). Calculate its total mechanical energy just before hitting the ground.
Solution: Given; Mass, (m = 4 kg) ; Height, (h = 10 m) ; Acceleration due to gravity, (g = 9.8 m/s2)
Gravitational Potential Energy (U) is given by:
\(\displaystyle U = mgh \)
Substituting the given values:
\(\displaystyle U = 4 \times 9.8 \times 10 = 392 \, \text{J}\)
At the initial position, the block has no kinetic energy. Therefore, the total mechanical energy is (392 J).
Example 4: A ball is thrown vertically upward with an initial velocity of (20 m/s). If the mass of the ball is (0.5 kg), calculate its total mechanical energy at the highest point.
Solution: Given; Initial velocity, (vi = 20 m/s); Mass, (m = 0.5 kg); Acceleration due to gravity, (g = 9.8 m/s2)
At the highest point, the velocity of the ball is (0 m/s). Kinetic energy (K) is given by:
\(\displaystyle K = \frac{1}{2} mv^2 \)
At the highest point, kinetic energy is (0 J). At the highest point, the ball has maximum potential energy, which is equal to the initial kinetic energy.
Therefore, the total mechanical energy is equal to the initial kinetic energy, which is
\(\displaystyle K = \frac{1}{2} \times 0.5 \times (20)^2 = 100 \, \text{J}\).
Example 5: A 2 kg mass is attached to a spring with a spring constant of (400 N/m). If the spring is compressed by (0.05 m) and the mass is released, calculate the maximum kinetic energy attained by the mass.
Solution: Given; Mass, (m = 2 kg); Spring constant, (k = 400 N/m); Displacement, (x = 0.05 m)
Elastic Potential Energy (U) stored in the spring is given by:
\(\displaystyle U = \frac{1}{2} k x^2 \)
Substituting the given values:
\(\displaystyle U = \frac{1}{2} \times 400 \times (0.05)^2 \)
\(\displaystyle U = \frac{1}{2} \times 400 \times 0.0025 \)
\(\displaystyle U = 0.25 \, \text{J} \)
At the initial position, the mass has no kinetic energy. So, the total mechanical energy is (0.25 J). When the spring is released, all the potential energy is converted into kinetic energy at the maximum compression. Therefore, the maximum kinetic energy is (0.25 J).
FAQs
What is potential energy, and how does it differ from kinetic energy?
Potential energy is energy that is stored in an object due to its position or configuration. It can be converted into kinetic energy when the object moves. Unlike kinetic energy, which depends on the object’s motion, potential energy depends on factors like height, position, or deformation of an object.
How is gravitational potential energy related to an object’s position?
Gravitational potential energy is the energy stored in an object due to its position relative to a reference point in a gravitational field, such as the surface of the Earth. The higher an object is above the reference point, the greater its gravitational potential energy, since it has the potential to fall and gain kinetic energy.
Can you explain how to calculate gravitational potential energy?
Gravitational potential energy (GPE) can be calculated using the formula: GPE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above the reference point. This formula quantifies the energy stored in an object due to its position in a gravitational field.
What factors affect the elastic potential energy stored in a spring?
Elastic potential energy is the energy stored in a stretched or compressed elastic material, such as a spring or a rubber band. The amount of elastic potential energy stored depends on factors such as the stiffness (spring constant) of the material and the amount of deformation (compression or elongation) it undergoes.
How does the spring constant affect the elastic potential energy of a spring?
The spring constant (k) is a measure of the stiffness of a spring or elastic material. It determines how much force is required to stretch or compress the spring by a certain amount. The greater the spring constant, the more elastic potential energy is stored in the spring for a given deformation.
Can elastic potential energy be converted into other forms of energy?
Yes, elastic potential energy can be converted into kinetic energy or other forms of energy. For example, when a compressed spring is released, it returns to its original shape and releases the stored elastic potential energy as kinetic energy, causing the spring to move or perform work on another object.
How does understanding potential energy contribute to engineering and design?
Understanding potential energy, including gravitational and elastic potential energy, is essential in engineering and design. Engineers use this knowledge to design structures, machinery, and systems that efficiently store, transfer, and utilize energy. For example, architects consider gravitational potential energy when designing tall buildings to ensure structural stability and safety. Similarly, designers use elastic potential energy principles in various applications, such as springs in suspension systems or energy storage devices.