Work-Energy Theorem

The concept of the Work-Energy Theorem has been recognized for centuries, but it was not always stated in its current form. It evolved from Newton’s second law applied to particles and extended to rigid bodies.

The Work-Energy Theorem is a fundamental principle in physics that has been recognized for centuries. However, it wasn’t always stated in its current form, and its development involved a series of twists and turns.

The roots of the Work-Energy Theorem can be traced back to the early understandings of force and motion. Philosophers and scientists like Aristotle and Galileo made observations about the nature of movement and the forces that cause it.

The theorem as we know it today evolved from Sir Isaac Newton’s laws of motion, particularly the second law, which connects force, mass, and acceleration. Newton’s insights laid the groundwork for understanding how forces act on objects and how these forces can change an object’s motion and energy.

During the 18th and 19th centuries, the concept of work and energy began to take a more scientific form. Scientists started to quantify the idea of “work” and relate it to the kinetic energy of objects. This period saw the development of the Work-Energy Theorem, which states that the work done by all forces acting on a particle equals the change in the particle’s kinetic energy.

The modern formulation of the Work-Energy Theorem was developed as scientists recognized that work transfers energy from one place to another or one form to another. This understanding allowed for the extension of the theorem to more general systems beyond just particles, including rigid bodies and rotational motion.

What is the Work-Energy Theorem?

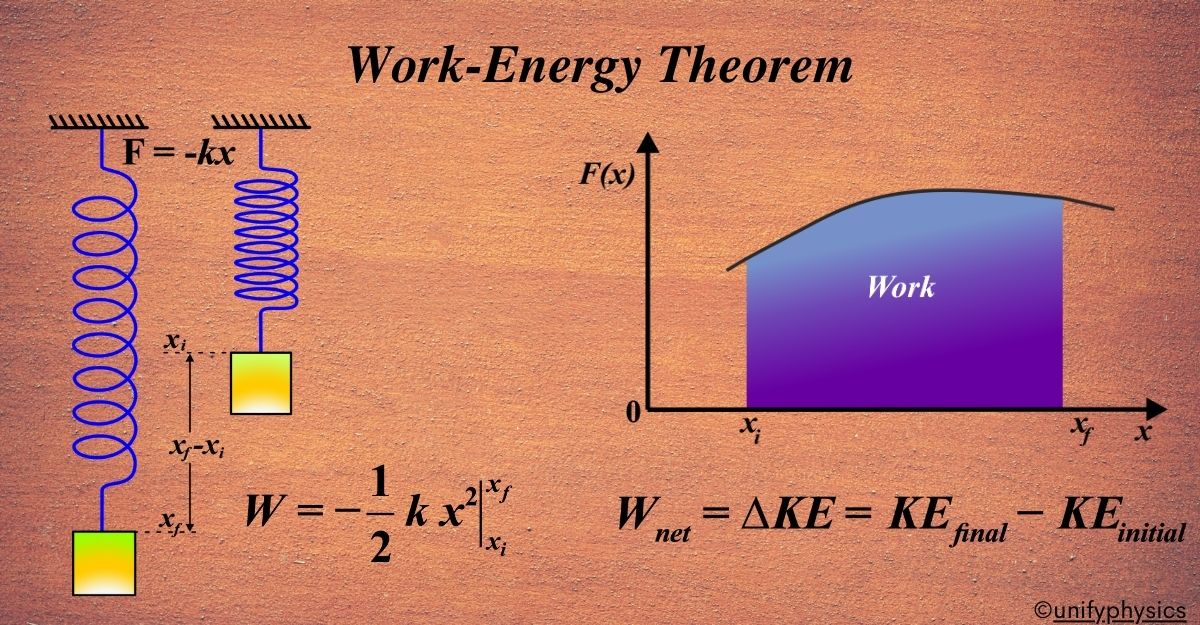
The Work-Energy Theorem is a fundamental principle in physics that connects two important concepts: work and energy. It tells us about the relationship between the work done on an object and the change in its kinetic energy. It states that the net work done by all forces acting on an object is equal to the change in the object’s kinetic energy.

Think of kinetic energy as the energy of motion. Any object that’s moving has kinetic energy. Now, when you apply a force to this object and move it, you’re doing work on it. According to the Work-Energy Theorem, the work you do on the object changes its kinetic energy.

The theorem can be expressed with a simple formula:

\(\displaystyle W_{\text{net}} = \Delta KE \)

• (W_net): This stands for the net work done on an object. It’s the total work from all forces acting on the object, whether pushing or pulling it.
• (∆KE): This represents the change in kinetic energy of the object. Kinetic energy is the energy an object has because of its motion.

The net work done on an object is equal to the change in its kinetic energy. If the kinetic energy increases, the work done is positive. If the kinetic energy decreases, the work done is negative.

The change in kinetic energy (∆KE) is then calculated as:

\(\displaystyle \Delta KE = KE_{\text{final}} – KE_{\text{initial}} \)

Example: Let’s say a skateboard starts from rest (so its initial kinetic energy is 0) and then you push it, doing 100 Joules of work. The final kinetic energy of the skateboard will be 100 Joules because:

\(\displaystyle W_{\text{net}} = \Delta KE = KE_{\text{final}} – KE_{\text{initial}} = 100 \, \text{J} – 0 \, \text{J} = 100 \, \text{J} \)

• If you push a skateboard and it speeds up, you’ve increased its kinetic energy, which means you’ve done positive work.
• If you pull back on the skateboard and it slows down, you’ve decreased its kinetic energy, which means you’ve done negative work.

Imagine you’re riding a bicycle down a hill. As you go down, the bicycle picks up speed, so its kinetic energy increases. The work done by gravity as you move down the hill is equal to the increase in your kinetic energy.

The Work-Energy Theorem is like a bridge that links the force you apply to an object with the energy of motion that the object gains or loses. It’s a powerful tool in physics that helps us understand how forces affect the motion and energy of objects in our world.

Derivation of Work-Energy Theorem

The theorem is derived from Newton’s second law, which connects force, mass, and acceleration. By integrating the force over the distance an object travels, we can relate it to the change in kinetic energy.

The Work-Energy Theorem tells us that the work done by all the forces acting on an object results in a change in the object’s kinetic energy. We begin with Newton’s second law of motion, which states that the force applied to an object is equal to the mass of the object times its acceleration:

\(\displaystyle F = ma \)

Next, we use a kinematic equation that relates the object’s final velocity (v), initial velocity (u), acceleration (a), and displacement (s):

\(\displaystyle v^2 = u^2 + 2as \)

We rearrange the kinematic equation to solve for acceleration:

\(\displaystyle 2as = v^2 – u^2 \)

\(\displaystyle a = \frac{v^2 – u^2}{2s} \)

Now, we substitute the expression for acceleration back into Newton’s second law:

\(\displaystyle F = m \left( \frac{v^2 – u^2}{2s} \right) \)

The work done (W) by the force is the force multiplied by the displacement (s):

\(\displaystyle W = F \cdot s \)

Substituting the force from above, we get:

\(\displaystyle W = m \left( \frac{v^2 – u^2}{2s} \right) s \)

\(\displaystyle W = \frac{1}{2} m (v^2 – u^2) \)

Kinetic energy (KE) is given by the formula:

\(\displaystyle KE = \frac{1}{2} mv^2 \)

The change in kinetic energy (( \Delta KE )) is the final kinetic energy minus the initial kinetic energy:

\(\displaystyle \Delta KE = KE_{\text{final}} – KE_{\text{initial}} \)

\(\displaystyle \Delta KE = \frac{1}{2} mv^2 – \frac{1}{2} mu^2 \)

Comparing the expression for work done with the change in kinetic energy, we see they are the same:

\(\displaystyle W = \Delta KE \)

This is the Work-Energy Theorem, which states that the work done by the forces on an object is equal to the change in the object’s kinetic energy.

Work-Energy Theorem for Constant Force

When a constant force acts on an object, it causes the object to accelerate and move in the direction of the force. The Work-Energy Theorem helps us understand how this force changes the kinetic energy of the object.

Let’s consider an object of mass (m) moving under the influence of a constant force (F). This force gives the object an acceleration (a), and let’s say the object moves a distance (s) from its initial position.

We know from Newton’s second law that (F = ma). There’s a kinematic equation that relates the final velocity (v) to the initial velocity (u), acceleration (a), and displacement (s):

\(\displaystyle v^2 = u^2 + 2as \)

Work done (W) by the force is the force multiplied by the displacement in the direction of the force. So, we have:

\(\displaystyle W = F \cdot s \)

Now, we substitute (a) from the kinematic equation into the work equation:

\(\displaystyle W = m \cdot a \cdot s \)

\(\displaystyle W = m \cdot \frac{v^2 – u^2}{2s} \cdot s \)

\(\displaystyle W = \frac{1}{2} m (v^2 – u^2) \)

Remember, kinetic energy (KE) is given by:

\(\displaystyle KE = \frac{1}{2} mv^2 \)

The change in kinetic energy ( \Delta KE ) is the final kinetic energy minus the initial kinetic energy:

\(\displaystyle \Delta KE = \frac{1}{2} mv^2 – \frac{1}{2} mu^2 \)

Comparing the expression for work done with the change in kinetic energy, we see they are the same:

\(\displaystyle W = \Delta KE \)

This derivation shows that the work done by a constant force on an object is equal to the change in the object’s kinetic energy.

Work-Energy Theorem for Variable Force

When the force acting on an object changes in magnitude or direction as the object moves, we call it a variable force. The Work-Energy Theorem can still be applied, but the calculation of work done is a bit more complex.

We know that work done (W) is the integral of force (F) over the displacement (s). For a variable force, this becomes:

\(\displaystyle W = \int F \cdot ds \)

If the force varies with displacement, we express it as (F(x)), where (x) is the displacement.

For a very small displacement (dx), the work done (dW) is approximately the force at that point times the small displacement:

\(\displaystyle dW = F(x) \cdot dx \)

To find the total work done by the variable force over a certain displacement from (x_i) to (x_f), we integrate the infinitesimal work:

\(\displaystyle W = \int_{x_i}^{x} F(x_f) \cdot dx \)

The total work done by the force is equal to the change in kinetic energy of the object. So, we have:

\(\displaystyle \Delta KE = \int_{x_i}^{x} F(x_f) \cdot dx \)

This equation tells us that the change in kinetic energy of an object is the area under the force-displacement graph from the initial to the final position.

Imagine you’re stretching a spring. The force required increases as you stretch it more. The work done to stretch the spring from its natural length to a certain point is the area under the force-displacement curve for the spring, which corresponds to the increase in kinetic energy if the spring were to release and move an object.

The Work-Energy Theorem for variable force shows that even when forces change as an object moves, the total work done by these forces still equals the change in the object’s kinetic energy.

Applications of the Work-Energy Theorem

The Work-Energy Theorem is not just a theoretical concept; it has practical applications in various fields of physics and engineering. Here are some of the key applications:

• Mechanics: In mechanics, the theorem is used to analyze the motion of objects. It helps us understand how the forces acting on an object, like gravity and friction, affect its kinetic energy and motion.
• Thermodynamics: The theorem plays a role in thermodynamics by relating mechanical work to changes in energy states, which is essential for understanding heat engines and energy cycles.
• Technological Innovations: It is applied in technological innovations that involve energy transfer and conversion, such as in the design of motors, vehicles, and even roller coasters.
• Sports: In sports, the Work-Energy Theorem helps in analyzing the performance of athletes, and understanding how energy is transferred in activities like running, jumping, or throwing.
• Accident Reconstruction: The theorem is used in accident reconstruction to determine the speeds involved in collisions based on the damage and energy transfer during the impact.
• Engineering: Engineers use the Work-Energy Theorem to design more efficient machines and structures by understanding the energy transformations that occur during operation.
• Physics Education: It’s a fundamental tool in physics education, helping students connect the dots between force, work, energy, and motion in a tangible way.

Advantages of Work-Energy Theorem

The theorem allows us to calculate other quantities like acceleration, force, or velocity if one is known. It helps to determine the energy used to move an object from one place to another.

• The theorem simplifies the process of solving problems involving forces and motion. Instead of dealing with forces and accelerations directly, you can use energy concepts to find solutions more easily.
• It eliminates the need to know the time over which the work was done. This is particularly useful in problems where time is not given or is difficult to determine.
• The theorem focuses on displacement rather than the path taken. This means you can calculate the work done and energy changes without knowing the detailed path of the object.
• It provides a direct link between the kinetic energy of an object and the work done on it, helping to understand how energy is transferred and conserved.
• The theorem has practical applications in mechanics, engineering, sports science, and more. It helps professionals and scientists analyze systems and predict outcomes based on energy changes.
• It reinforces the concept of energy conservation, showing that energy is not lost but transformed from one form to another.
• The theorem can be extended to include potential energy, allowing for a complete analysis of mechanical energy in a system.

Disadvantages of Work-Energy Theorem

The theorem does not apply in all spatial planes and only works for solid objects or rigid bodies. It does not provide complete information about the cause of motion and is based on scalar quantities, so the direction of force or velocity cannot be determined.

• The theorem is not applicable in all spatial planes. It works best for objects moving in a straight line or for rotational motion where we can define a clear rotational axis.
• It’s designed to work only for solid objects or rigid bodies. This means it doesn’t apply to systems where the shape of the object changes significantly during motion, like in fluids or deformable bodies.
• The theorem provides a quantitative measure of the change in kinetic energy but does not give complete information about the cause of motion. It tells us how much energy is transferred, but not why or how the forces are causing this transfer.
• It’s based on scalar quantities; hence, the direction of force or velocity cannot be determined from the theorem alone. This means it doesn’t give us the full picture of the dynamics involved in the motion of objects.
• The theorem focuses on kinetic energy and work done by forces, but it does not directly account for other forms of energy like potential energy or thermal energy unless they are specifically included in the analysis.
• It is sometimes referred to as the scalar form of Newton’s second law of motion. While it relates work and kinetic energy, it does not provide insights into the dynamics of the motion, which are described by Newton’s laws.

Also Read: Work

Solved Examples

Example 1: A force of 50 N is applied to a box of mass 5 kg, initially at rest, and moved horizontally for a distance of 10 meters. Calculate the final velocity of the box using the work-energy theorem.

Solution : Given: Force, (F = 50) N ; Mass, (m = 5) kg ; Distance, (d = 10) m

Work done by the force (W) is given by (W = F. d )

\(\displaystyle W = 50 \times 10 = 500 \, \text{J} \)

According to the work-energy theorem, the work done on the box is equal to its change in kinetic energy.

\(\displaystyle W = \Delta KE \)
\(\displaystyle 500 = \frac{1}{2} m v_f^2 \)
\(\displaystyle v_f^2 = \frac{2 \times 500}{5} = 200 \)
\(\displaystyle v_f = \sqrt{200} \approx 14.14 \, \text{m/s} \)

Example 2: A car of mass 1200 kg accelerates from rest to a speed of 20 m/s at a distance of 100 meters. Calculate the net work done on the car using the work-energy theorem.

Solution : Given; Mass of the car, (m = 1200) kg ; Initial velocity, (v_i = 0) m/s ; Final velocity, (v_f = 20) m/s ; Distance, (d = 100) m

Using the equation of motion \(\displaystyle v_f^2 = v_i^2 + 2ad \):

\(\displaystyle (20)^2 = (0)^2 + 2 \times a \times 100 \)
\(\displaystyle a = \frac{(20)^2}{200} = 2 \, \text{m/s}^2 \)

Now, using the work-energy theorem, the net work done is equal to the change in kinetic energy.

\(\displaystyle W = \Delta KE = \frac{1}{2} m v_f^2 – \frac{1}{2} m v_i^2 \)
\(\displaystyle W = \frac{1}{2} \times 1200 \times (20)^2 – \frac{1}{2} \times 1200 \times (0)^2 \)
\(\displaystyle W = 24000 \, \text{J} \)

Example 3: A block of mass 2 kg is dropped from a height of 10 meters. Calculate its velocity just before hitting the ground using the work-energy theorem.

Solution : Given; Mass of the block, (m = 2) kg ; Initial velocity, (v_i = 0 ) m/s ; Height, (h = 10) m ; Acceleration due to gravity, (g = 9.8) m/s²

Using the equation of motion \(\displaystyle v_f^2 = v_i^2 + 2gh \):

\(\displaystyle v_f^2 = 0 + 2 \times 9.8 \times 10 \)
\(\displaystyle v_f = \sqrt{196} = 14 \, \text{m/s} \)

Example 4: A spring with a spring constant of (200 N/m) is compressed by (0.1 m). Calculate the speed of a (0.5 kg) block when it leaves the spring using the work-energy theorem.

Solution : Given; Spring constant, (k = 200 N/m) ; Displacement of the spring, (x = 0.1 m) ; Mass of the block, (m = 0.5 kg)

The potential energy stored in the spring when compressed is given by \(\displaystyle PE = \frac{1}{2} kx^2 \).

\(\displaystyle PE = \frac{1}{2} \times 200 \times (0.1)^2 = 1 \, \text{J} \)

By the work-energy theorem, this potential energy is converted into the kinetic energy of the block at the moment it leaves the spring.

\(\displaystyle KE = \frac{1}{2} m v_f^2 = PE \)
\(\displaystyle \frac{1}{2} \times 0.5 \times v_f^2 = 1 \)
\(\displaystyle v_f^2 = 4 \)
\(\displaystyle v_f = 2 \, \text{m/s} \)

Example 5: A skier of mass (70 kg) starts from rest at the top of a slope that is (30 m) high. Calculate the speed of the skier at the bottom of the slope using the work-energy theorem. (Assume no friction.)

Solution : Given; Mass of the skier, (m = 70 kg) ; Height of the slope, (h = 30 m) ; Acceleration due to gravity, (g = 9.8 m/s²)

The potential energy at the top of the slope is converted into kinetic energy at the bottom.

\(\displaystyle PE = mgh = 70 \times 9.8 \times 30 = 20580 \, \text{J} \)

According to the work-energy theorem, (KE = PE).

\(\displaystyle \frac{1}{2} m v_f^2 = 20580 \)
\(\displaystyle v_f^2 = \frac{2 \times 20580}{70} \)
\(\displaystyle v_f = \sqrt{588} \approx 24.25 \, \text{m/s} \)

Problem 6: A rocket of mass (1000 kg) is launched vertically upwards with an initial speed of (200 m/s). If the rocket’s engine produces a constant thrust of (5000 N), calculate the maximum height reached using the work-energy theorem.

Solution: Given; Mass of the rocket, (m = 1000 kg) ; Initial velocity, (v_i = 200 m/s) ; Thrust produced by the engine, (F = 5000 N) ; Acceleration due to gravity, (g = 9.8 m/s²)

At the maximum height, the final velocity of the rocket becomes (0) m/s. Using the work-energy theorem:

\(\displaystyle W_{\text{engine}} – W_{\text{gravity}} = \Delta KE \)

\(\displaystyle Fd – mgh = \frac{1}{2} mv_f^2 \)

\(\displaystyle 5000d – 1000 \times 9.8 \times h = \frac{1}{2} \times 1000 \times 0^2 \)

\(\displaystyle 5000d – 1000 \times 9.8 \times h = 0 \)

\(\displaystyle d = h \)

Therefore, the maximum height reached by the rocket is (d = h).

\(\displaystyle h = \frac{v_i^2}{2g} = \frac{200^2}{2 \times 9.8} \)
\(\displaystyle h \approx 2040.82 \, \text{m} \)

FAQs