Long before Newton, ancient civilizations had their interpretations of gravitational phenomena. The Greeks, for example, observed that objects fall towards the Earth and theorized about the nature of celestial bodies. However, it was not until the Renaissance that significant progress was made.
In the late 16th and early 17th centuries, Galileo Galilei made crucial observations. He discovered that objects of different masses fall at the same rate in the absence of air resistance. This was a radical departure from the Aristotelian view that heavier objects fall faster.
Johannes Kepler, a contemporary of Galileo, formulated three laws of planetary motion based on meticulous astronomical observations. These laws described how planets orbit the Sun but did not explain why they moved as they did.
Isaac Newton was the first to propose a universal law that applied to all objects, both celestial and terrestrial. Building on the work of his predecessors, Newton proposed that every particle of matter in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
Newton published his law of universal gravitation in the “Philosophiæ Naturalis Principia Mathematica” in 1687. This publication is considered one of the most significant works in the history of science. It not only presented the law of gravitation but also laid the foundation for classical mechanics.
The first experimental test of Newton’s law in the laboratory was conducted by Henry Cavendish in 1798, over a century after Newton’s initial publication. Cavendish’s experiment measured the force of attraction between masses and helped to determine the value of the gravitational constant.
While Newton’s law has been superseded by Einstein’s theory of general relativity, it remains a powerful tool for understanding the forces that govern the motions of most celestial bodies. It is only in the realm of very strong gravitational fields or at very small scales that relativity becomes necessary.
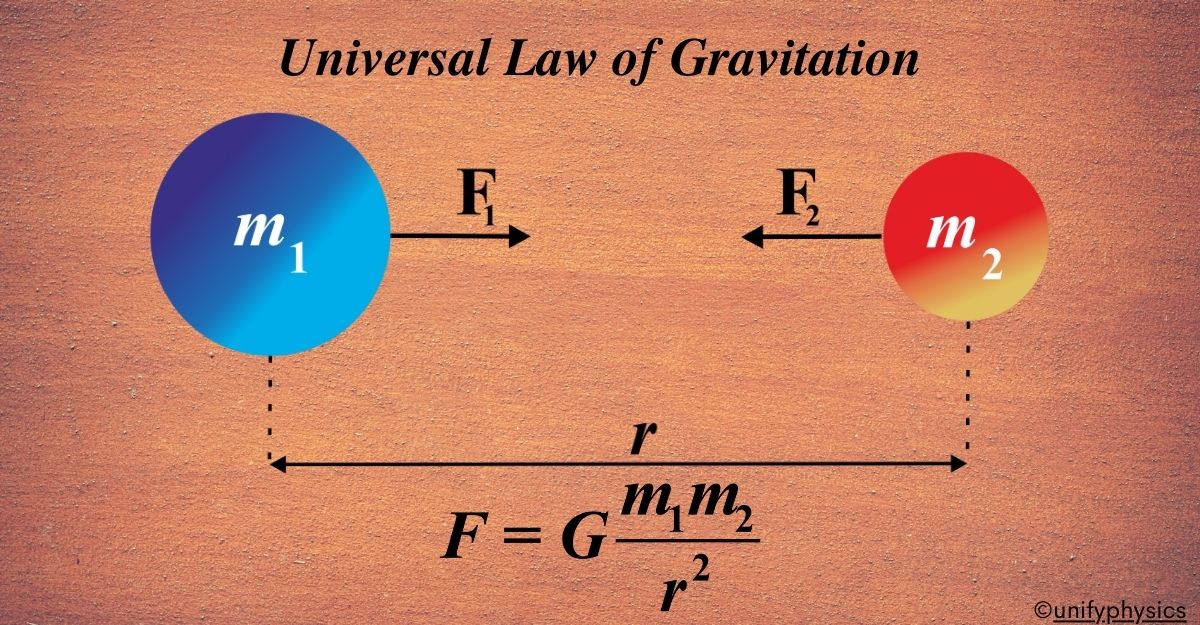
What is the Universal Law of Gravitation?
Statement
” Every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The force acts along the line joining the two masses.”
The Universal Law of Gravitation is like a cosmic rule that tells us how objects in the universe interact with each other through the force of gravity. Imagine every object in the universe has invisible strings attached to every other object. These strings represent the gravitational force. The strength of the pull from these strings depends on two things: how massive the objects are and how far apart they are.
The more massive an object is the stronger its gravitational pull. It’s like having a stronger magnet. So, a basketball has a weaker pull compared to the Earth because the Earth is much more massive.
The farther apart two objects are, the weaker the gravitational pull between them. If you stretch the string too far, it doesn’t pull as much. This is why astronauts feel weightless in space; they are far from the Earth’s surface, so gravity’s pull on them is weaker.
Newton gave us a neat formula to calculate this gravitational force:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} \)
- F stands for the gravitational force between two objects.
- G is the gravitational constant, a number that makes our calculations accurate.
- (m1) and (m2) are the masses of the two objects we’re considering.
- r is the distance between the centers of the two objects.
So, when you’re sitting in class, the Earth pulls on you, and you pull on the Earth too! But because the Earth is so massive and you’re relatively close to it, you feel a strong pull towards the ground. That’s gravity at work, and it’s described by the Universal Law of Gravitation.
This law helps us understand not just why apples fall from trees, but also how the moon orbits the Earth and how planets stay in their paths around the sun. It’s a fundamental principle that shows us gravity is a universal force acting everywhere in the cosmos.
The Universal Law of Gravitation provides a quantitative description of the force of attraction between any two objects with mass. The force of gravity is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centers. This means that larger masses experience a stronger gravitational force, and the force weakens rapidly as objects move farther apart. Gravity is an attractive force, always acting along the line joining the centers of the two masses. This means that objects with mass are drawn toward each other.
- Falling Objects: The Universal Law of Gravitation explains why objects fall to the ground when released. The Earth’s gravitational pull pulls objects toward its center.
- Planetary Orbits: This law is crucial for understanding the orbits of planets around the Sun. The gravitational force between the Sun and a planet keeps the planet in orbit.
Gravitational force is the driving factor behind the motion of celestial bodies. It governs the orbits of planets around the Sun, the moons around planets, and the interactions between galaxies. Sir Isaac Newton’s formulation of the Universal Law of Gravitation revolutionized our understanding of these celestial dynamics.
Example: Imagine you’re sitting under an apple tree, and you see a ripe apple let go of its branch and start falling to the ground. This everyday occurrence might seem simple, but it’s a perfect example of how gravity works, as described by the Universal Law of Gravitation.
In this scenario, we have two main players: the Earth and the Apple. Earth, being much larger, has a more powerful gravitational pull. The apple, even though it’s smaller, still has mass, and that means gravity is at play for it too.
Masses Involved:
- Mass of the Earth (mEarth),
- Mass of the apple (mapple).
The distance from the center of the Earth to the center of the apple (r). The gravitational force (F) pulling the apple toward the Earth is given by Newton’s law.
The distance between the center of the Earth and the center of the apple is the key parameter influencing the strength of the gravitational force. As the apple falls, this distance decreases, intensifying the gravitational attraction between the two masses. Newton’s law of gravitation comes into play, expressing the force (F) pulling the apple toward the Earth. The formula,
\(\displaystyle F=G.\frac{{{{m}{{Earth}}}.{{m}{{apple}}}}}{{{{r}^{2}}}}\)
outlines the intricate relationship between the masses, the gravitational constant (G), and the square of the distance between their centers. While the mass of the apple is considerably smaller than the Earth, the force exerted by the Earth’s gravity significantly influences the apple’s acceleration. The gravitational force acts as an invisible hand, guiding the apple downward, and the acceleration experienced by the apple is a testament to the gravitational pull defined by Newton’s laws.
This example underscores the universality of the law of gravitation, showing that the same principles governing celestial bodies also shape the behavior of everyday objects on Earth. The Universal Law of Gravitation helps us understand why things fall, making it an essential concept for explaining both everyday events and the movements of celestial bodies in the universe.
Gravitational Constant
When we talk about the Universal Law of Gravitation, there’s a special number that always comes into play — the Gravitational Constant, denoted by (G). Let’s understand what it is and why it’s so important:
Think of the Gravitational Constant as the cosmic glue that holds everything together. It’s the number that determines the strength of the pull of gravity between two objects.
The Value of (G): The Gravitational Constant (G) has a value of approximately (\(\displaystyle 6.674 \times 10^{-11}\)) Newton meter squared per kilogram squared (N m²/kg²). This might seem like a tiny number, but it’s mighty because it works across the vastness of space.
Why Do We Need ( G )?: Without (G), we wouldn’t be able to calculate the force of gravity between objects. Newton’s formula for gravitational force is:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} \)
Here, (F) is the force of gravity, (m1) and (m2) are the masses of the objects, and (r) is the distance between their centers. (G) is what makes this equation work for any two objects in the universe, whether they’re apples or planets.
How Was ( G ) Determined?: The Gravitational Constant was first measured by Henry Cavendish in the late 18th century using a delicate experiment involving a torsion balance. This experiment allowed him to measure the tiny gravitational attraction between two lead spheres and thus determine the value of (G).
(G) is a fundamental constant in physics. It appears in many equations and calculations related to gravity, from the orbits of planets to the behavior of objects on Earth. It’s a key part of understanding how the universe works at both the large scale of galaxies and the small scale of atoms.
The Universal Law of Gravitation states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
According to Newton’s second law of motion:
\(\displaystyle\text{Total force} = \text{object’s mass} \times \text{object’s acceleration}\)
For gravitational force, (Fg) is the force of gravity acting on an object.
\(\displaystyle F_g \propto m\)
where (m) is the object’s mass. Consider two objects with masses (m) and (M). The gravitational force (Fg) between these objects is proportional to the product of their masses.
\(\displaystyle F_g \propto m \times M\)
The gravitational force is also inversely proportional to the square of the distance (r) between the centers of the two objects.
\(\displaystyle F_g \propto \frac{1}{r^2}\)
Combining these two proportionalities, we get:
\(\displaystyle F_g \propto \frac{m \times M}{r^2}\)
To convert this into an equation, we introduce a proportionality constant (G), known as the gravitational constant.
\(\displaystyle F_g = G \frac{m \times M}{r^2}\)
The gravitational constant (G) is a universal constant with a value of approximately (\(\displaystyle 6.674 \times 10^{-11} \, \text{N} \, (\text{m}^2/\text{kg}^2) \)).
\(\displaystyle F_g = G \frac{m \times M}{r^2}\)
Let’s consider the Earth and an object (say a satellite).
- Earth’s Mass (M): The mass of Earth is approximately (\(\displaystyle 5.972 \times 10^{24} \, \text{kg} \)).
- Object’s Mass (m): Suppose the mass of the satellite is (1000 kg).
- Distance (r): The average distance from the center of the Earth to the satellite (at low Earth orbit) is about (\(\displaystyle 6.371 \times 10^6 \, \text{m} \)).
Using the gravitational formula:
\(\displaystyle F_g = G \frac{m \times M}{r^2}\)
Plug in the values:
\(\displaystyle F_g = (6.674 \times 10^{-11} \, \text{N} \, \text{m}^2/\text{kg}^2) \frac{(1000 \, \text{kg}) \times (5.972 \times 10^{24} \, \text{kg})}{(6.371 \times 10^6 \, \text{m})^2}\)
This calculation will yield the gravitational force (Fg) acting on the satellite due to the Earth. Newton’s Universal Law of Gravitation is fundamental to understanding how planets move around the sun, how satellites orbit Earth, and generally how objects interact through gravity.
The Importance of the Universal Law of Gravitation
The importance of the Universal Law of Gravitation is like discovering the hidden strings that connect everything in the universe. Here’s why this law is so crucial:
Explains Celestial Movements: The law explains why planets orbit the sun, why moons orbit planets, and why galaxies hold together. It’s the reason we have predictable patterns in the sky, which ancient civilizations relied on for calendars and navigation.
The basis for Modern Physics: Newton’s law laid the groundwork for classical mechanics, which is essential for understanding how objects move and interact. It’s a stepping stone to more advanced theories, like Einstein’s General Relativity.
Everyday Life Applications: Gravity affects everything we do, from playing sports to building structures. Understanding gravity helps engineers design safer buildings and bridges, and it’s also why your feet stay on the ground instead of floating off into space.
Space Exploration: This law is used to calculate the trajectories of spacecraft, enabling missions to other planets and moons. It helps us send satellites into orbit, which provide GPS, weather forecasting, and telecommunications.
Understanding Tides: The gravitational pull of the moon and the sun on Earth’s oceans leads to tides, which are crucial for marine life and have been vital for human navigation and exploration throughout history.
Advances in Technology: Gravitational principles are at the heart of many modern technologies. For example, understanding gravity is essential in designing accelerometers, which are used in smartphones, vehicles, and gaming controllers.
Educational Foundation: For students, grasping this law is fundamental to their education in physics. It not only helps them understand the universe but also prepares them for further studies in science and engineering fields.
The Universal Law of Gravitation Applications
This law isn’t just a theory; it has real-world uses that affect our daily lives and scientific advancements. Here are some key applications:
Space Exploration: The law helps scientists calculate the gravitational forces between Earth and other celestial bodies. This is crucial for sending satellites into orbit and planning space missions. It ensures that spacecraft can enter, remain in, or leave an orbit around a planet.
GPS Technology: Satellites used for GPS need to maintain precise orbits to provide accurate location data. The Universal Law of Gravitation is used to understand the gravitational influences on these satellites, which helps in keeping them on the correct path.
Predicting Tides: The gravitational pull of the moon and the sun on Earth’s oceans causes tides. By applying this law, we can predict high and low tides, which is vital for coastal navigation and fishing industries.
Understanding Planetary Motion: The law explains the orbits of planets around the sun and moons around planets. It’s the reason why we have seasons, and eclipses, and can predict celestial events with high accuracy.
Measuring Earth’s Mass: Using the Universal Law of Gravitation, scientists can calculate the mass of Earth by observing the gravitational pull it exerts on objects. This is essential for various calculations in geophysics and engineering.
Discovering New Planets: Astronomers use this law to detect new planets outside our solar system. They observe the gravitational effects these planets have on their stars, such as slight wobbles, to infer their presence.
Engineering and Construction: Engineers take into account the force of gravity when designing buildings, bridges, and other structures. It’s essential for ensuring stability and safety in construction projects.
Studying Black Holes and Galaxies: The law is fundamental in astrophysics for understanding the dynamics of galaxies and the nature of black holes, which are regions of space with extremely strong gravitational forces.
By understanding these applications, students can see how the Universal Law of Gravitation extends beyond the classroom and into various fields, shaping our understanding of the universe and enabling technological advancements.
Also Read: Kepler’s Law of Planetary Motion
Solved Examples
Problem 1: Calculate the gravitational force between two masses, (m1 = 10 kg) and (m2 = 20 kg), separated by a distance of (2 m).
Solution: The gravitational force (F) between two masses is given by Newton’s Universal Law of Gravitation:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} \)
Where (G) is the gravitational constant, (\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)).
Given: m1 = 10 kg; m2 = 20 kg; r = 2 m
Calculate (F):
\(\displaystyle F = 6.674 \times 10^{-11} \frac{10 \times 20}{2^2} \)
\(\displaystyle F = 6.674 \times 10^{-11} \frac{200}{4} \)
\(\displaystyle F = 6.674 \times 10^{-11} \times 50 \)
\(\displaystyle F = 3.337 \times 10^{-9} \, \text{N} \)
Therefore, the gravitational force between the two masses is (\(\displaystyle 3.337 \times 10^{-9} \, \text{N}\)).
Problem 2: Calculate the gravitational acceleration on the surface of a planet with a mass of (\(\displaystyle 5 \times 10^{24} \, \text{kg}\)) and a radius of (\(\displaystyle 6 \times 10^6 \, \text{m}\)).
Solution: Gravitational acceleration (g) on the surface of a planet is given by:
\(\displaystyle g = G \frac{M}{R^2} \)
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)
\(\displaystyle M = 5 \times 10^{24} \, \text{kg} \)
\(\displaystyle R = 6 \times 10^6 \, \text{m} \)
Calculate (g):
\(\displaystyle g = 6.674 \times 10^{-11} \frac{5 \times 10^{24}}{(6 \times 10^6)^2} \)
\(\displaystyle g = 6.674 \times 10^{-11} \frac{5 \times 10^{24}}{36 \times 10^{12}} \)
\(\displaystyle g = 6.674 \times 10^{-11} \times \frac{5}{36} \times 10^{12} \)
\(\displaystyle g = 6.674 \times 10^{-11} \times 0.1389 \times 10^{12} \)
\(\displaystyle g = 0.926 \, \text{m/s}^2 \)
Therefore, the gravitational acceleration on the surface of the planet is (\(\displaystyle 0.926 \, \text{m/s}^2\)).
Problem 3: Calculate the orbital velocity of a satellite orbiting the Earth at an altitude of (300 km) above the surface. The radius of the Earth is (\(\displaystyle 6.371 \times 10^6 \, \text{m}\)) and the mass of the Earth is (\(\displaystyle 5.972 \times 10^{24} \, \text{kg}\)).
Solution: The orbital velocity (v) of a satellite is given by:
\(\displaystyle v = \sqrt{\frac{GM}{R}} \)
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)
\(\displaystyle M = 5.972 \times 10^{24} \, \text{kg} \)
\(\displaystyle R = R_{\text{Earth}} + \text{altitude} = 6.371 \times 10^6 + 300 \times 10^3 \, \text{m} \)
Calculate (R):
\(\displaystyle R = 6.371 \times 10^6 + 300 \times 10^3 \)
\(\displaystyle R = 6.671 \times 10^6 \, \text{m} \)
Calculate (v):
\(\displaystyle v = \sqrt{\frac{6.674 \times 10^{-11} \times 5.972 \times 10^{24}}{6.671 \times 10^6}} \)
\(\displaystyle v = \sqrt{\frac{3.986 \times 10^{14}}{6.671 \times 10^6}} \)
\(\displaystyle v = \sqrt{5.978 \times 10^7} \)
\(\displaystyle v = 7.73 \times 10^3 \, \text{m/s} \)
Therefore, the orbital velocity of the satellite is (\(\displaystyle 7.73 \times 10^3 \, \text{m/s}) or (7.73 \, \text{km/s}\)).
Problem 4: Calculate the escape velocity from a planet with a mass of (\(\displaystyle 4 \times 10^{24} \, \text{kg}\)) and a radius of (\(\displaystyle 4 \times 10^6 \, \text{m}\)).
Solution: The escape velocity (ve) is given by:
\(\displaystyle v_e = \sqrt{\frac{2GM}{R}} \)
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)
\(\displaystyle M = 4 \times 10^{24} \, \text{kg} \)
\(\displaystyle R = 4 \times 10^6 \, \text{m} \)
Calculate (ve):
\(\displaystyle v_e = \sqrt{\frac{2 \times 6.674 \times 10^{-11} \times 4 \times 10^{24}}{4 \times 10^6}} \)
\(\displaystyle v_e = \sqrt{\frac{5.3392 \times 10^{14}}{4 \times 10^6}} \)
\(\displaystyle v_e = \sqrt{1.3348 \times 10^8} \)
\(\displaystyle v_e = 1.156 \times 10^4 \, \text{m/s} \)
Therefore, the escape velocity from the planet is (\(\displaystyle 1.156 \times 10^4 \, \text{m/s}) or (11.56 \, \text{km/s}\)).
Problem 5: Calculate the gravitational potential energy of a system consisting of two masses (\(\displaystyle m_1 = 5 \times 10^3 \, \text{kg}\)) and (\(\displaystyle m_2 = 3 \times 10^3 \, \text{kg}\)), separated by a distance of (10m).
Solution: The gravitational potential energy (U) between two masses is given by:
\(\displaystyle U = -G \frac{m_1 m_2}{r} \)
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)
\(\displaystyle m_1 = 5 \times 10^3 \, \text{kg} \)
\(\displaystyle m_2 = 3 \times 10^3 \, \text{kg} \)
r = 10 m
Calculate (U):
\(\displaystyle U = -6.674 \times 10^{-11} \frac{5 \times 10^3 \times 3 \times 10^3}{10} \)
\(\displaystyle U = -6.674 \times 10^{-11} \frac{15 \times 10^6}{10} \)
\(\displaystyle U = -6.674 \times 10^{-11} \times 1.5 \times 10^6 \)
\(\displaystyle U = -1.0011 \times 10^{-4} \, \text{J} \)
Therefore, the gravitational potential energy of the system is (\(\displaystyle -1.0011 \times 10^{-4} \, \text{J}\)).
Problem 6: A mass of (10 kg) is on the surface of two different planets. Planet X has a mass of (\(\displaystyle 6 \times 10^{24} \, \text{kg}\)) and a radius of (\(\displaystyle 6 \times 10^6 \, \text{m}\)), while Planet Y has a mass of (\(\displaystyle 3 \times 10^{24} \, \text{kg}\)) and a radius of (\(\displaystyle 3 \times 10^6 \, \text{m}\)). Compare the gravitational forces acting on the mass of both planets.
Solution: Gravitational force (F) on the surface of a planet is given by:
\(\displaystyle F = G \frac{Mm}{R^2} \)
$latex \displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} )
m = 10 kg
For Planet X:
\(\displaystyle M_X = 6 \times 10^{24} \, \text{kg} \)
\(\displaystyle R_X = 6 \times 10^6 \, \text{m} \)
Calculate (FX):
\(\displaystyle F_X = 6.674 \times 10^{-11} \frac{6 \times 10^{24} \times 10}{(6 \times 10^6)^2} \)
\(\displaystyle F_X = 6.674 \times 10^{-11} \frac{60 \times 10^{24}}{36 \times 10^{12}}\)
\(\displaystyle F_X = 6.674 \times 10^{-11} \times 1.667 \times 10^{13} \)
\(\displaystyle F_X = 111.31 \, \text{N} \)
For Planet Y:
\(\displaystyle M_Y = 3 \times 10^{24} \, \text{kg} \)
\(\displaystyle R_Y = 3 \times 10^6 \, \text{m} \)
Calculate (FY):
\(\displaystyle F_Y = 6.674 \times 10^{-11} \frac{3 \times 10^{24} \times 10}{(3 \times 10^6)^2} \)
\(\displaystyle F_Y = 6.674 \times 10^{-11} \frac{30 \times 10^{24}}{9 \times 10^{12}} \)
\(\displaystyle F_Y = 6.674 \times 10^{-11} \times 3.333 \times 10^{13} \)
\(\displaystyle F_Y = 222.62 \, \text{N} \)
Therefore, the gravitational force acting on the mass on Planet X is (111.31 N), and on Planet Y is (222.62 N).
FAQs
What is the Universal Law of Gravitation?
The Universal Law of Gravitation, formulated by Sir Isaac Newton, states that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This fundamental law explains the gravitational attraction between objects, regardless of their size or distance apart.
Why is the Universal Law of Gravitation considered ‘universal’?
The law is termed ‘universal’ because it applies to all objects with mass, regardless of their location in the universe. It describes the gravitational force between any two masses, whether they are planets, stars, or particles of dust, making it a fundamental principle in understanding the mechanics of the cosmos.
How did Newton derive the Universal Law of Gravitation?
Newton derived the Universal Law of Gravitation through observations and mathematical reasoning. He built upon the work of previous scientists like Johannes Kepler, who described planetary motions, and Galileo Galilei, who studied the motion of objects. Newton’s insight was to realize that the same force causing an apple to fall from a tree also governs the motion of the moon and the planets.
What are the implications of the Universal Law of Gravitation for planetary motion?
The Universal Law of Gravitation explains why planets orbit the sun in elliptical paths and why moons orbit planets. It accounts for the stable orbits of celestial bodies and the forces that keep them in their respective paths. This law provides the foundation for understanding the dynamics of the solar system and the motion of satellites.
How does the Universal Law of Gravitation explain the tides on Earth?
The Universal Law of Gravitation explains tides as the result of the gravitational pull exerted by the moon and the sun on Earth’s oceans. The moon’s gravity causes water to bulge out on the side of Earth closest to it, creating a high tide. Simultaneously, inertia creates a similar bulge on the opposite side of the Earth, resulting in another high tide. The interaction between these gravitational forces and the Earth’s rotation leads to the regular rise and fall of sea levels.
Can the Universal Law of Gravitation be used to predict the motion of artificial satellites?
Yes, the Universal Law of Gravitation is crucial for predicting and calculating the orbits of artificial satellites around Earth. By knowing the mass of Earth and the satellite, and the distance between them, scientists can determine the gravitational force and the necessary velocity for the satellite to maintain a stable orbit. This understanding is essential for satellite deployment and operation.
What is the significance of the Universal Law of Gravitation in modern science?
The Universal Law of Gravitation has immense significance in modern science as it provides a comprehensive framework for understanding gravitational interactions. It has been fundamental in the development of classical mechanics, celestial mechanics, and astrophysics. It also underpins technologies such as GPS and satellite communications, and it continues to influence contemporary research in cosmology and space exploration.