The understanding of gravity has evolved over centuries, with contributions from many great minds that have shaped our current knowledge. The earliest thoughts on gravity date back to Aristotle in ancient Greece, who believed that objects fall towards the Earth due to their nature. Later, in the 6th century, the Indian astronomer Brahmagupta described gravity as an attractive force.
The Renaissance brought a significant shift in the understanding of gravity with the work of Galileo Galilei. He challenged Aristotle’s views and, through his experiments, concluded that all objects fall at the same rate regardless of their mass.
The most significant leap came from Sir Isaac Newton in the 17th century. He proposed the Law of Universal Gravitation, which states that every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This was a groundbreaking concept that provided a mathematical explanation for both terrestrial and celestial phenomena.
In the early 20th century, Albert Einstein revolutionized our understanding of gravity with his Theory of General Relativity. He described gravity not as a force, but as a curvature of spacetime caused by the presence of mass and energy. This theory provided a more comprehensive explanation for gravitational phenomena, including the bending of light by gravity.
Each new theory has built upon the previous ones, expanding our comprehension of the universe and its laws. This chronology highlights the importance of questioning, experimentation, and mathematical formulation in the advancement of scientific knowledge.
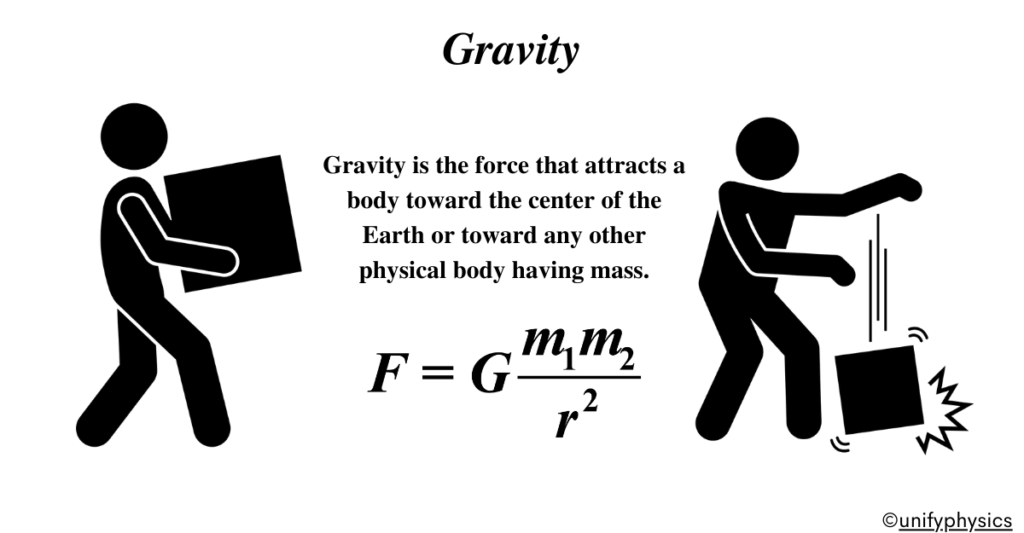
What Is Gravity?
Gravity is the force that holds the universe together. It’s what keeps your feet on the ground and the planets in motion. Gravity is one of the four fundamental forces of nature, alongside electromagnetism, and the strong and weak nuclear forces. It is the force that attracts two bodies towards each other. Here’s a breakdown of the concept:
Gravity is universal; it acts between any two pieces of matter in the universe, no matter how large or small they are. This means that gravity is not just the reason why objects fall to the ground, but it’s also the force that keeps the planets in their orbits around the Sun and the Moon in their orbit around Earth.
You can’t see gravity, but you can certainly feel its effects. It’s the invisible force that pulls objects toward each other. For instance, it’s what keeps you firmly on the ground and causes an apple to fall from a tree.
The strength of the gravitational pull between two objects depends on their masses. The more massive an object is the stronger its gravitational pull. That’s why the very massive Earth has a significant gravitational pull, while a small object like a tennis ball has a very weak pull.
Gravity also depends on the distance between two objects. The closer two objects are to each other, the stronger the gravitational pull. As the distance increases, the force of gravity decreases.
Gravity is essential for the structure and evolution of the universe. It’s responsible for the formation of stars, planets, and galaxies. Without gravity, the universe as we know it would not exist.
On our planet, the force of gravity gives weight to physical objects and is responsible for the ocean tides. The standard acceleration due to gravity at the Earth’s surface, denoted as (g), is approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)).
Albert Einstein’s theory of general relativity describes gravity not as a force, but as a curvature of spacetime around massive objects. According to this theory, massive objects like stars and planets warp the space around them, and other objects move along these curves, which is perceived as gravitational attraction. It’s a fundamental force that is essential for the existence of everything from stars and planets to humans and apples.
Measuring Gravity
Gravity is not just a theoretical concept; it has practical implications and can be measured. Here’s how we can understand the measurement of gravity: The gravitational force between two objects can be calculated using Newton’s Law of Universal Gravitation. The formula is:
\(\displaystyle F = G \frac{m_1 m_2}{r^2} \)
- (F) is the gravitational force between two masses,
- (G) is the gravitational constant (\(\displaystyle6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\)),
- (m1) and (m2) are the masses of the two objects,
- (r) is the distance between the centers of the two masses.
On Earth, we often measure gravity in terms of the acceleration it gives to freely falling objects. This is denoted as (g) and is approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)) at the Earth’s surface. This means that in the absence of air resistance, an object will accelerate downwards at this rate.
Scientists use instruments called gravimeters to measure the acceleration due to gravity. These devices can be very sophisticated and are used to detect tiny variations in gravitational acceleration. Students can perform simple experiments to measure gravity. For example, by timing how long it takes for an object to fall a known distance, they can calculate the acceleration due to gravity using the equation:
\(\displaystyle d = \frac{1}{2} g t^2 \)
- (d) is the distance,
- (g) is the acceleration due to gravity,
- (t) is the time it takes for the object to fall.
Understanding how to measure gravity is crucial for various applications, such as determining the mass distribution within Earth, finding oil and mineral deposits, and even for navigation purposes.
What is Free Fall?:
Free fall is a term used in physics to describe the motion of an object that is moving solely under the influence of gravity. In free fall, an object is subject to no forces other than gravity. This means that the object’s motion is not affected by air resistance or any other force. It’s important to note that this is an idealized concept; in the real world, air resistance always plays some role.
Characteristics of Free Fall
- Acceleration: All objects in free fall (on Earth) accelerate downwards at a rate of approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)), which is the acceleration due to gravity.
- Mass Independence: The acceleration due to gravity is the same for all objects, regardless of their mass. This means that if you dropped a feather and a hammer from the same height in a vacuum (where there is no air resistance), they would hit the ground at the same time.
In physics classrooms, free fall can be demonstrated using a vacuum chamber or with the help of a strobe light demonstration that eliminates the visual effects of air resistance, allowing students to observe the constant acceleration due to gravity.
The motion of a freely falling object can be described using kinematic equations. For an object starting from rest, the distance (d) it falls in time (t) is given by:
\(\displaystyle d = \frac{1}{2} g t^2 \)
where (g) is the acceleration due to gravity.
Examples:
- Astronauts in Orbit: Astronauts aboard the International Space Station experience weightlessness because they are in a state of continuous free fall toward Earth, but their forward motion keeps them in orbit.
- Skydiving: A skydiver before opening their parachute is in a state of free fall, though in reality, air resistance plays a significant role.
Gravity on Earth
Gravity is the force that attracts objects towards the center of the Earth. It’s what gives us weight and keeps us from floating off into space. Gravity is an invisible force that pulls objects toward each other. Earth’s gravity is what keeps you on the ground and what makes things fall. It’s also responsible for the ocean tides, as the gravitational pull of the moon causes the seas to rise and fall.
The gravity on Earth comes from all its mass. All this mass makes a combined gravitational pull on all the mass in your body, giving you weight. If you were on a planet with less mass than Earth, you would weigh less than you do here.
Gravity not only pulls on mass but also light. If you shine a flashlight upwards, the light will grow imperceptibly redder as gravity pulls it. This effect, predicted by Einstein, is measurable though not visible to the naked eye.
Gravity isn’t the same everywhere on Earth. It’s slightly stronger over places with more mass underground than over places with less mass. NASA uses spacecraft to measure these variations in Earth’s gravity, which helps scientists create maps of gravity variations on Earth.
Gravity is what holds the planets in orbit around the sun and what keeps the moon in orbit around Earth. It creates stars and planets by pulling together the material from which they are made.
Gravity Varies:
Gravity on Earth varies slightly depending on where you are. The equator experiences a slightly weaker gravitational pull due to the centrifugal force from the Earth’s rotation and the increased distance from the Earth’s center. In contrast, the poles experience a stronger gravitational pull due to the absence of centrifugal force and their proximity to the Earth’s center.
Gravity at the Equator:
- Centrifugal Force: At the equator, the Earth’s rotation generates a centrifugal force that acts outwardly. This force is strongest at the equator because it’s the point farthest from the axis of rotation.
- Reduced Gravity: The centrifugal force effectively reduces the net gravitational pull experienced by objects. As a result, gravity is slightly weaker at the equator compared to other parts of the Earth.
Gravity at the Poles:
- No Centrifugal Reduction: At the poles, there is no centrifugal force acting outwardly because they are on the axis of rotation. Therefore, objects at the poles don’t experience this reduction in gravitational pull.
- Closer to Earth’s Center: The Earth is not a perfect sphere but an oblate spheroid, meaning it’s slightly flattened at the poles and bulges at the equator. This shape causes the poles to be closer to the center of the Earth, increasing the gravitational pull there.
Why Gravity Varies? The Earth’s shape means that the surface at the equator is farther from the center of mass than the surface at the poles. Since gravitational force decreases with distance, gravity is stronger at the poles. The rotation of the Earth affects the gravitational force. The centrifugal force due to Earth’s rotation counteracts gravity more at the equator than at the poles, leading to a slight variation in the strength of gravity.
Gravitational Measurements: Scientists can measure the difference in gravity using sensitive instruments. These measurements show that the acceleration due to gravity is about (\(\displaystyle 9.78 \, \text{m/s}^2 \)) at the equator and (\(\displaystyle 9.83 \, \text{m/s}^2 \)) at the poles.
Because gravity is slightly stronger at the poles, a person would weigh more at the poles than at the equator, assuming their mass remains constant.
Acceleration due to gravity (g)
Acceleration due to gravity is the measure of how fast an object accelerates towards the Earth when it’s in free fall. Acceleration due to gravity (g) is the acceleration experienced by an object near the Earth’s surface due to gravity’s force. This acceleration is directed towards the center of the Earth and has a magnitude of approximately 9.8 m/s 2.
In the absence of air resistance, all objects near the Earth’s surface experience the same acceleration due to gravity regardless of their mass. Galileo famously demonstrated this principle when he dropped objects of different masses from the Leaning Tower of Pisa.
The direction of acceleration due to gravity is always towards the center of the Earth. When an object is thrown upwards, the acceleration due to gravity acts in the opposite direction to the motion, gradually slowing it down until it reaches its highest point. The formula to calculate acceleration due to gravity is:
Whether an object is dropped, thrown upwards, or projected horizontally, the acceleration due to gravity always acts towards the center of the Earth. The force of gravity (F) on an object with mass (m) near the Earth’s surface is (\(\displaystyle F = m \times g \)).
The formula for (g) based on the universal law of gravitation is:
\(\displaystyle g = \frac{G \times m_{\text{earth}}}{R^2} \)
where (G) is the gravitational constant, (\(\displaystyle m_{\text{earth}} \)) is the mass of the Earth, and (R) is the radius of the Earth. For most practical purposes, (g) is approximated as (\(\displaystyle 9.8 \, \text{m/s}^2 \)).
In free fall, an object’s velocity increases by (\(\displaystyle 9.8 \, \text{m/s} \)) every second due to (g). Projectile motion (g) affects the trajectory of projectiles, causing them to follow a curved path under the influence of gravity.
Variation of Acceleration due to Gravity
The acceleration due to gravity (g) is generally considered constant near the surface of the Earth, with an average value of approximately 9.8 m/s2. However, it’s essential to note that g can vary under different circumstances and conditions. Here are some factors that can lead to variations in the acceleration due to gravity:
Variation with altitude
Acceleration due to gravity (g) is the rate at which an object accelerates when it is in free fall, solely under the influence of Earth’s gravitational pull. At the surface of the Earth, (g) is approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)). As we move away from the Earth’s surface—up a mountain, in an airplane, or towards space (g) decreases.
Why Does (g) Change with Altitude? The strength of gravity follows an inverse-square law, which means it decreases with the square of the distance from the center of the Earth.
The formula that represents this variation is:
$$ g_h = g_0 \left( \frac{R}{R + h} \right)^2 $$
where (gh) is the acceleration due to gravity at height (h) above the Earth’s surface, (g0) is the standard acceleration due to gravity at the Earth’s surface, and (R) is the radius of the Earth.
At the top of Mount Everest, (g) is slightly less than (\(\displaystyle 9.8 \, \text{m/s}^2 \)) because the mountain’s summit is further from the Earth’s center than the surface at sea level.
This variation is crucial for calculating the orbits of satellites. The higher a satellite is, the less the gravitational pull, and the faster it must travel to remain in orbit. Astronauts experience weightlessness in space because they are far enough from the Earth that ( g ) is significantly weaker, creating a microgravity environment.
If we were to graph (g) against altitude, we would see a curve that starts at (\(\displaystyle 9.8 \, \text{m/s}^2 \)) and gradually decreases as altitude increases. By understanding how (g) varies with altitude, students can better grasp the concept of gravitational fields and how they influence the motion of objects on Earth and in space.
As you move away from the Earth’s surface, such as going to higher altitudes or climbing a mountain, the distance from the center of the Earth increases. According to the gravitational force formula,
\(\displaystyle F=G.\frac{{{{m}_{1}}.{{m}_{2}}}}{{{{r}^{2}}}}\)
an increase in r leads to a decrease in the gravitational force. Consequently, the acceleration due to gravity (g) decreases slightly with altitude.
The acceleration due to gravity (g0) at the Earth’s surface can be expressed using the Earth’s mass (M) and radius (R):
\(\displaystyle g_{0} = G \frac{M}{R^2} \)
When an object is at an altitude (h) above the Earth’s surface, the distance from the Earth’s center is (R + h). The acceleration due to gravity at this altitude (gh) is:
\(\displaystyle g_{h} = G \frac{M}{(R + h)^2} \)
We can substitute the expression for (g0) into our equation for (gh):
\(\displaystyle g_{h} = \frac{g_0 R^2}{(R + h)^2} \)
\(\displaystyle g_{h} = g_{0} \left( \frac{R}{R + h} \right)^2 \)
This is the expression for the variation of acceleration due to gravity with altitude. It shows that as you increase your altitude (h), the acceleration due to gravity (gh) decreases because the distance from the Earth’s center increases, and gravity decreases with the square of the distance.
Variation Factor \(\displaystyle {{\left( {\frac{R}{{R+h}}} \right)}^{2}}\):
This factor shows how the acceleration due to gravity, (g), changes as you move to a higher altitude above the Earth’s surface. Gravity decreases with the square of the distance from the Earth’s center.
At Sea Level: When (h = 0), the factor is (1), so (gh = g0), which is the standard (\(\displaystyle 9.8 \, \text{m/s}^2 \)).
At Higher Altitudes: As (h) increases, the denominator (R+h) becomes larger, making the entire fraction smaller. When squared, this fraction reduces (g0) to (gh), showing that gravity decreases with altitude.
- Mountains vs. Sea Level: On top of a mountain, (h) is greater, so (gh) will be less than (g0). This means you’d weigh slightly less on a mountain than at sea level.
- Astronauts in Space: For astronauts in orbit, (h) is very large compared to (R), so the factor significantly reduces (g), creating a microgravity environment.
If we graph (gh) against (h), the curve starts at (g0) and decreases as (h) increases, reflecting the \(\displaystyle \left( \frac{R}{R+h} \right)^2\) relationship.
Variation with depth
Acceleration due to gravity (g) is the rate at which an object accelerates towards the center of the Earth due to Earth’s gravitational pull. At the surface of the Earth, (g) is approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)). As we go below the Earth’s surface, into a mine or a deep well for example, (g) decreases.
When you’re on the surface, the entire mass of the Earth is pulling you towards its center. As you go deeper, there’s less mass beneath you pulling you down, and more mass above you pulling you up. At any depth, the gravitational pull from the mass of the Earth’s shell above you cancels out. Only the mass in the sphere below you contributes to the gravitational pull.
The formula that expresses this variation is:
\(\displaystyle g_{depth} = g \left(1 – \frac{d}{R}\right) \)
where (gdepth) is the acceleration due to gravity at depth (d), (g) is the standard acceleration due to gravity at the Earth’s surface, and (R) is the radius of the Earth.
Understanding how (g) varies with depth is important for engineering projects that involve underground construction. Scientists use the variation of (g) with depth to study the Earth’s interior and to locate mineral deposits. If we graph (gdepth) against (d), we would see a linear decrease from (g) at the surface to zero at the Earth’s center.
To derive the expression for the variation of acceleration due to gravity with depth, we’ll consider how gravity changes as you go beneath the Earth’s surface.
According to Newton’s Shell Theorem, when you are at a depth (d) inside the Earth, only the mass of the Earth that is at a radius smaller than (R – d) (where (R) is the Earth’s radius) contributes to the gravitational force. The mass outside of your depth level exerts no net gravitational force on you.
If we assume the Earth has a uniform density (ρ), then the mass (Md) inside the radius (R – d) is:
\(\displaystyle M_d = \rho \times \frac{4}{3}\pi (R – d)^3 \)
The acceleration due to gravity (gd) at depth ( d ) is proportional to the mass ( Md) and inversely proportional to the square of the radius (R – d):
\(\displaystyle g_d = G \frac{M_d}{(R – d)^2} \)
\(\displaystyle g_d = G \frac{\rho \times \frac{4}{3}\pi (R – d)^3}{(R – d)^2} \)
\(\displaystyle g_d = G \frac{\rho \times \frac{4}{3}\pi (R – d)}{1} \)
The density (ρ) can be related to the acceleration due to gravity at the Earth’s surface (g0) by considering the total mass (M) of the Earth:
\(\displaystyle M = \rho \times \frac{4}{3}\pi R^3 \)
\(\displaystyle g_0 = G \frac{M}{R^2} \)
\(\displaystyle g_0 = G \frac{\rho \times \frac{4}{3}\pi R^3}{R^2} \)
\(\displaystyle g_0 = G \rho \times \frac{4}{3}\pi R \)
Now, we can express (gd) using (g0):
\(\displaystyle g_d = g_0 \frac{(R – d)}{R} \)
\(\displaystyle g_d = g_0 \left(1 – \frac{d}{R}\right) \)
This is the expression for the variation of acceleration due to gravity with depth. It shows that as you go deeper into the Earth ((d) increases), the acceleration due to gravity (gd) decreases linearly with depth. This derivation helps students understand how gravity is not a constant force throughout the Earth and changes depending on your location within it.
Variation Due to Rotation of Earth
The rotation of the Earth influences its shape, creating an oblate spheroid. At the equator, the centrifugal force caused by the Earth’s rotation counteracts some of the gravitational force, leading to a decrease in g compared to the poles. The variation due to rotation is more pronounced at the equator.
As the Earth rotates, any object on its surface is in circular motion. This motion generates a centrifugal force that acts outwardly, away from the axis of rotation. This centrifugal force effectively reduces the gravitational pull experienced by objects on the Earth’s surface.
- At the Equator: The centrifugal force is greatest at the equator because this is where the linear speed due to Earth’s rotation is the fastest. Therefore, the acceleration due to gravity is slightly less at the equator.
- Towards the Poles: As you move towards the poles, the centrifugal force decreases because the linear speed due to Earth’s rotation decreases—consequently, the acceleration due to gravity increases.
The effective acceleration due to gravity (geff) at any latitude ( \(\displaystyle\phi\) ) can be expressed as:
\(\displaystyle g_{eff} = g – R\omega^2\cos^2(\phi) \)
where (g) is the acceleration due to gravity without the rotation effect, (R) is the Earth’s radius, (\(\displaystyle \omega \)) is the angular velocity of Earth’s rotation, and ( \(\displaystyle\phi \)) is the latitude.
This means that an object would weigh slightly less at the equator than at the poles, due to the variation in (geff) caused by Earth’s rotation. Engineers and scientists must account for this variation when designing structures and systems, such as GPS satellites, that are sensitive to gravitational forces.
If we were to graph (geff) against latitude, we would see a curve that starts lower at the equator and increases towards the poles.
To derive the expression for the variation of acceleration due to gravity due to the rotation of the Earth, we’ll consider the centrifugal force that arises from Earth’s rotation and how it affects gravitational acceleration.
When an object is on the surface of the rotating Earth, it experiences a centrifugal force outward from the axis of rotation. This force is given by:
\(\displaystyle F_{cent} = mR\omega^2\cos^2(\phi) \)
where (m) is the mass of the object, (R) is the radius of the Earth, ( \(\displaystyle\omega\) ) is the angular velocity of Earth’s rotation, and ( \(\displaystyle\phi \)) is the latitude.
The centrifugal acceleration (acent) that corresponds to this force is:
\(\displaystyle a_{cent} = R\omega^2\cos^2(\phi) \)
The gravitational acceleration (g) at the Earth’s surface without the rotation effect is approximately (\(\displaystyle 9.8 \, \text{m/s}^2 \)).
The effective gravitational acceleration (geff) that an object feels is the gravitational acceleration minus the centrifugal acceleration:
\(\displaystyle g_{eff} = g – a_{cent} \)
\(\displaystyle g_{eff} = g – R\omega^2\cos^2(\phi) \)
Substituting the expression for (acent) into the equation for (geff), we get the final expression:
\(\displaystyle g_{eff} = g – R\omega^2\cos^2(\phi) \)
This expression shows that the effective acceleration due to gravity decreases with the increase in latitude from the equator to the poles due to the centrifugal force caused by Earth’s rotation. At the equator (\(\displaystyle\phi = 0 \)), the centrifugal acceleration is at its maximum, and as we move towards the poles (\(\displaystyle\phi = 90^\circ \)), the centrifugal acceleration becomes zero, and (geff) approaches (g).
By understanding this derivation, students can appreciate the interplay between rotational motion and gravity, and how Earth’s rotation leads to a variation in the gravitational acceleration experienced at different latitudes.
Variation Due to the Shape of Earth
Earth is not a perfect sphere but an oblate spheroid. This means it is slightly flattened at the poles and bulges at the equator.
How Shape Affects Gravity
- Radius Variation: The radius of the Earth is larger at the equator than at the poles due to this bulging.
- Gravity’s Dependence on Radius: The acceleration due to gravity (g) is inversely proportional to the square of the radius (R) of the Earth. So, where the radius is larger, (g) is smaller, and vice versa.
The relationship between the gravitational acceleration at the poles (gp) and at the equator (ge) can be expressed as:
\(\displaystyle \frac{g_p}{g_e} = \frac{R_e^2}{R_p^2} \)
where (Re) is the equatorial radius, and (Rp) is the polar radius.
This means you would weigh slightly more at the poles than at the equator, not just because of the centrifugal force but also because of the Earth’s shape. The shape of the Earth must be taken into account when calculating satellite orbits, especially for those in low Earth orbit.
If we were to graph (g) against latitude, we would see a slight increase in (g) from the equator to the poles, reflecting the Earth’s oblate shape.
To derive the expression for the variation of acceleration due to gravity due to the shape of the Earth, we need to understand how the Earth’s oblateness affects gravitational acceleration.
The Earth is an oblate spheroid, meaning it’s slightly flattened at the poles and bulges at the equator. This causes the Earth’s equatorial radius (Re) to be larger than its polar radius (Rp).
The gravitational acceleration (g) at a point on the Earth’s surface is inversely proportional to the square of the distance from the Earth’s center to that point. At the poles, this distance is (Rp), and at the equator, it is (Re).
The gravitational acceleration at the poles (GP) and at the equator (ge) can be expressed as:
\(\displaystyle g_p = \frac{G M}{R_p^2} \)
\(\displaystyle g_e = \frac{G M}{R_e^2} \)
To find the relationship between (gp) and (ge), we take the ratio of the two expressions:
\(\displaystyle \frac{g_p}{g_e} = \frac{R_e^2}{R_p^2} \)
If we know the value of (gp), we can express (ge) as:
\(\displaystyle g_e = g_p \frac{R_p^2}{R_e^2} \)
The Earth’s oblateness is defined by the difference between the equatorial and polar radii. Let’s denote the oblateness factor as (f), where:
\(\displaystyle f = \frac{R_e – R_p}{R_p} \)
We can write the equatorial radius as:
\(\displaystyle R_e = R_p (1 + f) \)
Substituting (Re) in terms of (Rp) and (f) into the expression for (ge), we get:
\(\displaystyle g_e = g_p \frac{1}{(1 + f)^2} \)
This final expression shows that the gravitational acceleration at the equator (ge) is less than that at the poles (gp) due to the Earth’s oblateness. The factor (1 + f)2 accounts for the increase in radius and hence the decrease in gravitational acceleration at the equator.
Solved Examples
Problem 1: Calculate the acceleration due to gravity at an altitude of 500 km above the Earth’s surface. The radius of the Earth (R) is (\(\displaystyle 6.371 \times 10^6 \, \text{m} \)) and the standard acceleration due to gravity at the surface (g) is (\(\displaystyle 9.81 \, \text{m/s}^2 \)).
Solution: The acceleration due to gravity at a height (h) above the Earth’s surface is given by:
\(\displaystyle g_h = g \left( \frac{R}{R + h} \right)^2 \)
Given:
\(\displaystyle h = 500 \times 10^3 \, \text{m} = 500,000 \, \text{m} \)
\(\displaystyle R = 6.371 \times 10^6 \, \text{m} \)
\(\displaystyle g = 9.81 \, \text{m/s}^2 \)
Calculate (gh):
\(\displaystyle g_h = 9.81 \left( \frac{6.371 \times 10^6}{6.371 \times 10^6 + 500,000} \right)^2 \)
\(\displaystyle g_h = 9.81 \left( \frac{6.371 \times 10^6}{6.871 \times 10^6} \right)^2 \)
\(\displaystyle g_h = 9.81 \left( \frac{6.371}{6.871} \right)^2 \)
\(\displaystyle g_h = 9.81 \left( 0.927 \right)^2 \)
\(\displaystyle g_h = 9.81 \times 0.859 \)
\(\displaystyle g_h \approx 8.43 \, \text{m/s}^2 \)
Therefore, the acceleration due to gravity at an altitude of 500 km is approximately (\(\displaystyle 8.43 \, \text{m/s}^2 \)).
Also Read: Universal Law of Gravitation
Problem 2: Calculate the acceleration due to gravity at a depth of 1000 km below the Earth’s surface. The radius of the Earth (R) is (\(\displaystyle 6.371 \times 10^6 \, \text{m} \)).
Solution: The acceleration due to gravity at a depth (d) below the Earth’s surface is given by:
\(\displaystyle g_d = g \left( 1 – \frac{d}{R} \right) \)
Given:
\(\displaystyle d = 1000 \times 10^3 \, \text{m} = 1,000,000 \, \text{m} \)
\(\displaystyle R = 6.371 \times 10^6 \, \text{m} \)
\(\displaystyle g = 9.81 \, \text{m/s}^2 \)
Calculate (gd):
\(\displaystyle g_d = 9.81 \left( 1 – \frac{1,000,000}{6.371 \times 10^6} \right) \)
\(\displaystyle g_d = 9.81 \left( 1 – 0.157 \right) \)
\(\displaystyle g_d = 9.81 \times 0.843 \)
\(\displaystyle g_d \approx 8.27 \, \text{m/s}^2 \)
Therefore, the acceleration due to gravity at a depth of 1000 km is approximately (\(\displaystyle 8.27 \, \text{m/s}^2 \)).
Problem 3: Calculate the effective acceleration due to gravity at the equator considering the Earth’s rotation. The radius of the Earth (R) is (\(\displaystyle 6.371 \times 10^6 \, \text{m} \)) and the angular velocity ( \(\displaystyle\omega \)) of the Earth is (\(\displaystyle 7.27 \times 10^{-5} \, \text{rad/s} \)).
Solution: The effective acceleration due to gravity at the equator considering Earth’s rotation is given by:
\(\displaystyle g_{\text{eff}} = g – \omega^2 R \)
Given:
\(\displaystyle R = 6.371 \times 10^6 \, \text{m} \)
\(\displaystyle \omega = 7.27 \times 10^{-5} \, \text{rad/s} \)
\(\displaystyle g = 9.81 \, \text{m/s}^2 \)
Calculate ( \(\displaystyle\omega^2 R\)):
\(\displaystyle \omega^2 R = (7.27 \times 10^{-5})^2 \times 6.371 \times 10^6 \)
\(\displaystyle \omega^2 R = 5.29 \times 10^{-9} \times 6.371 \times 10^6 \)
\(\displaystyle \omega^2 R \approx 0.0336 \, \text{m/s}^2 \)
Calculate (\(\displaystyle g_{\text{eff}} \)):
\(\displaystyle g_{\text{eff}} = 9.81 – 0.0336 \)
\(\displaystyle g_{\text{eff}} \approx 9.7764 \, \text{m/s}^2 \)
Therefore, the effective acceleration due to gravity at the equator considering Earth’s rotation is approximately (\(\displaystyle 9.7764 \, \text{m/s}^2 \)).
Problem 4: Calculate the difference in acceleration due to gravity between the poles and the equator. Assume the acceleration due to gravity at the poles is (\(\displaystyle 9.832 \, \text{m/s}^2 \)) and at the equator is (\(\displaystyle 9.780 \, \text{m/s}^2 \)).
Solution: The difference in acceleration due to gravity between the poles and the equator is:
\(\displaystyle \Delta g = g_{\text{poles}} – g_{\text{equator}} \)
Given:
\(\displaystyle g_{\text{poles}} = 9.832 \, \text{m/s}^2 \)
\(\displaystyle g_{\text{equator}} = 9.780 \, \text{m/s}^2 \)
Calculate ( \(\displaystyle\Delta g \)):
\(\displaystyle \Delta g = 9.832 – 9.780 \)
\(\displaystyle \Delta g = 0.052 \, \text{m/s}^2 \)
Therefore, the difference in acceleration due to gravity between the poles and the equator is (\(\displaystyle 0.052 \, \text{m/s}^2 \)).
Problem 5: Calculate the acceleration due to gravity on the surface of a planet with a mass of (\(\displaystyle 3 \times 10^{24} \, \text{kg} \)) and a radius of (\(\displaystyle 2 \times 10^6 \, \text{m} \)).
Solution: The acceleration due to gravity on the surface of a planet is given by:
\(\displaystyle g = G \frac{M}{R^2} \)
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} \)
\(\displaystyle M = 3 \times 10^{24} \, \text{kg} \)
\(\displaystyle R = 2 \times 10^6 \, \text{m} \)
Calculate (g):
\(\displaystyle g = 6.674 \times 10^{-11} \frac{3 \times 10^{24}}{(2 \times 10^6)^2}\)
\(\displaystyle g = 6.674 \times 10^{-11} \frac{3 \times 10^{24}}{4 \times 10^{12}} \)
\(\displaystyle g = 6.674 \times 10^{-11} \times 0.75 \times 10^{12} \)
\(\displaystyle g = 6.674 \times 0.75 \times 10 \)
\(\displaystyle g = 5.0055 \, \text{m/s}^2 \)
Therefore, the acceleration due to gravity on the surface of the planet is approximately (\(\displaystyle 5.0055 \, \text{m/s}^2 \)).
Problem 6: Calculate the difference in gravitational potential energy for a mass of (10kg) when it is moved from the surface of the Earth to an altitude of 500 km. The radius of the Earth (R) is (\(\displaystyle 6.371 \times 10^6 \, \text{m} \)).
Solution: The gravitational potential energy at a distance (r) from the center of the Earth is given by:
\(\displaystyle U = -G \frac{M m}{r} \)
The difference in gravitational potential energy (\(\displaystyle \Delta U \)), when the mass is moved from the surface (R) to an altitude (R + h), is:
\(\displaystyle\Delta U = U_{\text{altitude}} – U_{\text{surface}} \)
\(\displaystyle \Delta U = -G \frac{M m}{R + h} + G \frac{M m}{R} \)
Given:
\(\displaystyle G = 6.674 \times 10^{-11} \, \text{N m}^2 \text{kg}^{-2} )
\)latex \displaystyle M = 5.972 \times 10^{24} \, \text{kg} )
m = 10 kg
\(\displaystyle R = 6.371 \times 10^6 \, \text{m} \)
\(\displaystyle h = 500 \times 10^3 \, \text{m} = 500,000 \, \text{m} \)
Calculate (\(\displaystyle U_{\text{surface}} \)) and (\(\displaystyle U_{\text{altitude}} \)):
\(\displaystyle U_{\text{surface}} = -6.674 \times 10^{-11} \frac{5.972 \times 10^{24} \times 10}{6.371 \times 10^6} \)
\(\displaystyle U_{\text{surface}} = -6.674 \times 10^{-11} \times 5.972 \times 10^{25} / 6.371 \times 10^6 \)
\(\displaystyle U_{\text{surface}} \approx -6.25 \times 10^8 \, \text{J} \)
\(\displaystyle U_{\text{altitude}} = -6.674 \times 10^{-11} \frac{5.972 \times 10^{24} \times 10}{6.871 \times 10^6} \)
\(\displaystyle U_{\text{altitude}} = -6.674 \times 10^{-11} \times 5.972 \times 10^{25} / 6.871 \times 10^6 \)
\(\displaystyle U_{\text{altitude}} \approx -5.79 \times 10^8 \, \text{J} \)
Calculate (\(\displaystyle \Delta U \)):
\(\displaystyle\Delta U = U_{\text{altitude}} – U_{\text{surface}}\)
\(\displaystyle\Delta U = (-5.79 \times 10^8) – (-6.25 \times 10^8) \)
\(\displaystyle\Delta U = 0.46 \times 10^8 \)
\(\displaystyle \Delta U = 4.6 \times 10^7 \, \text{J} \)
Therefore, the difference in gravitational potential energy is (\(\displaystyle 4.6 \times 10^7 \, \text{J} \)).
FAQs
What is gravity and how does it affect objects on Earth?
Gravity is the force of attraction between two masses. On Earth, it gives weight to physical objects and causes them to fall towards the ground when dropped. This force is what keeps us anchored to the planet and governs the motion of objects ranging from everyday items to celestial bodies.
What is meant by acceleration due to gravity (g)?
Acceleration due to gravity (denoted as (g)) is the acceleration experienced by an object due to the gravitational pull of Earth. It is the rate at which an object speeds up as it falls freely under the influence of Earth’s gravity, typically measured at 9.8 meters per second squared (m/s²) near the Earth’s surface.
How does the acceleration due to gravity vary with altitude?
The acceleration due to gravity decreases with increasing altitude. As you move further away from the Earth’s surface, the gravitational force weakens because the distance from the center of the Earth increases, resulting in a lower value of (g).
How does the acceleration due to gravity change with depth below the Earth’s surface?
The acceleration due to gravity decreases as you go deeper below the Earth’s surface. Inside the Earth, the effective mass attracting the object is reduced because only the mass beneath the object contributes to the gravitational pull. As a result, (g) diminishes as depth increases.
What effect does the Earth’s rotation have on the acceleration due to gravity?
The Earth’s rotation causes a variation in the acceleration due to gravity. At the equator, the centrifugal force due to Earth’s rotation slightly counteracts the gravitational pull, resulting in a smaller effect (g). At the poles, this effect is negligible, so (g) is stronger compared to the equator.
How does the shape of the Earth affect the acceleration due to gravity?
The Earth is not a perfect sphere but an oblate spheroid, meaning it is slightly flattened at the poles and bulging at the equator. This shape causes the gravitational force to vary, being stronger at the poles and weaker at the equator due to the increased distance from the Earth’s center.
Why is it important to understand the variations in the acceleration due to gravity?
Understanding the variations in the acceleration due to gravity is important for several reasons. It affects calculations in engineering, construction, and geophysics, and is crucial for accurate measurements in fields like satellite navigation and space exploration. It also helps in understanding natural phenomena such as tides and the behavior of objects at different locations on Earth.
