The concept of the Centre of Mass is deeply rooted in the work of ancient scholars and has evolved through the contributions of many great minds over the centuries.
The story of the Centre of Mass begins with the ancient Greek mathematician, physicist, and engineer Archimedes of Syracuse. Around the 3rd century BC, Archimedes made significant contributions to the understanding of the CoM. He is known for his work with levers and the principle of buoyancy, which relies heavily on the concept of CoM.
Archimedes used the idea of CoM to explain why different shapes of objects behave in a certain way when subjected to forces. He demonstrated that the torque exerted on a lever by weights at various points is the same as if all the weights were concentrated at their CoM. This principle made it easier to understand and predict the behavior of complex objects by simplifying them to a single point where all their mass seemed to be concentrated.
Over time, the concept of CoM was refined and expanded upon by other scholars. It became a cornerstone in the study of mechanics, particularly in understanding how objects balance and move. The CoM is crucial in the design of stable structures and in the analysis of the motion of bodies in space.
Today, the CoM is used in various fields, from engineering to astronomy. It helps engineers design vehicles and buildings by predicting how they will react to forces. Astronomers use the CoM to understand the orbits of planets and the motion of celestial bodies.
What is the Centre of Mass?
The Centre of Mass is the point in an object or system of particles where the entire mass can be considered as concentrated. It’s the average location of all the mass in the system.
Imagine you have a group of friends standing together for a group photo. Now, if you wanted to find the “average” position of everyone in that photo, you’d look for a point where everyone is equally distributed around it. That’s similar to what the Centre of Mass is in physics.
In technical terms, the Centre of Mass is a point where we can consider the entire mass of an object or a system of particles to be concentrated. It’s like the balancing point of the object. If you were to place your finger exactly at the CoM of a ruler, it would balance perfectly on your finger.
For a single object, the CoM is pretty straightforward—it’s usually at the geometric center. But for a system of particles or a complex shape, it’s the weighted average of their positions. When we say ‘weighted’, we mean that each particle’s contribution to the CoM is proportional to its mass. So, heavier particles pull the CoM closer to them.
Here’s a simple way to visualize it:
- If you have two weights connected by a rod, the CoM is closer to the heavier weight.
- If the weights are the same, the CoM is right in the middle of the rod.
The CoM is not always inside the material of the object. For example, the CoM of a doughnut is in the middle of the hole, where there’s no dough!
Why is the CoM important? Because it helps us predict how an object will behave when forces are applied. Whether it’s a spinning frisbee, a flying rocket, or a tumbling gymnast, knowing the CoM lets us understand and calculate their motion.
Centre of Mass Formula
The CoM formula helps us find the location of the CoM for a group of particles or a continuous mass distribution. It’s like finding the balance point of an object or system.
When we have separate particles, each with its own mass and position, we use the following formula:
\(\displaystyle\text{CoM} = \frac{\sum_{i=1}^{n} m_i x_i}{\sum_{i=1}^{n} m_i}\)
Here’s what each symbol means:
- (CoM): Centre of Mass
- (mi): Mass of the (ith) particle
- (xi): Position of the (ith) particle
- (n): Total number of particles
Think of it as a seesaw. If you have kids of different weights sitting at different distances from the pivot, where would you put the pivot so that the seesaw balances? That’s what the CoM formula calculates.
The CoM formula is a way to find the “average” location of mass in a system. For a bunch of particles, you multiply each mass by its position, add them all up, and then divide by the total mass. For a continuous object, you do a similar thing, but you add up all the tiny bits of mass and their positions using calculus.
Centre of Mass of a Body Having Continuous Mass Distribution
When we talk about continuous mass distribution, we’re referring to objects where the mass isn’t just at specific points but spread out over a volume, area, or length. Think of it like a thick slice of bread versus a pile of crumbs. The slice has mass all over, while the crumbs are like discrete masses.
To find the CoM for such an object, we can’t just add up the positions of individual masses because there are infinitely many tiny bits of mass. Instead, we use calculus, which is a way of adding up an infinite number of infinitesimally small things.
For an object with a continuous mass distribution, the position of the CoM is given by the integral:
\(\displaystyle\text{CoM} = \frac{1}{M} \int x \, dm\)
- (M) is the total mass of the object.
- (x) is the position.
- (dm) is an infinitesimally small amount of mass.
Imagine you have a long, stretchy rubber band. If you want to find the point where you can balance it on your finger, you need to consider every little bit of the rubber band’s mass. By integrating, you’re effectively doing that—considering each tiny piece, its position, and how much it ‘weighs’ (its mass).
Uniform Density:
If the object has uniform density, meaning the mass is spread out evenly, the CoM will be at the geometric center. This is because every part of the object contributes equally to the total mass.
Non-Uniform Density:
For objects with non-uniform density, where some parts are denser than others, the CoM shifts toward the denser areas. It’s like having a heavier weight on one side of a seesaw—it pulls the CoM toward it.
Take a loaf of bread as an example. If it’s a perfect, uniform loaf, the CoM is right in the middle. But if one end of the loaf is packed with more ingredients and hence denser, the CoM will be closer to that end.
Centre of Mass and Centre of Gravity
The Centre of Gravity is the point where the gravitational force can be considered to act. It coincides with the CoM when the gravitational field is uniform.
Centre of Mass (CoM): The CoM is a point in an object or system where we can consider all the mass to be concentrated. It’s the “average” location of all the mass in the body. For instance, if you have a uniform stick, the CoM is right in the middle because the mass is evenly distributed.
Centre of Gravity (CoG): The CoG is the point where the gravitational force effectively acts on an object. It’s like the “balance point” under gravity. If you have a uniform gravitational field (which is a good approximation near the Earth’s surface), the CoG is at the same point as the CoM.
The Relationship Between CoM and CoG: In a uniform gravitational field, the CoM and CoG coincide, meaning they are at the same point. This is because the gravitational force is equal across the object, so the “average” location of the gravitational pull is also the “average” location of the mass.
However, if the gravitational field is not uniform, like in space or near a large celestial body, the CoG might not be at the same point as the CoM. This is because the gravitational force could be stronger on one side of the object than the other, pulling the CoG towards it.
Examples:
- Uniform Stick: For a uniform stick lying horizontally, both the CoM and CoG are at the midpoint.
- Earth and Moon: The Earth’s CoM is at its geometric center, but the CoG is slightly towards the Moon due to the Moon’s gravitational pull.
Key Points to Remember:
- CoM is about the distribution of mass.
- CoG is about the distribution of weight under gravity.
- They are the same point in a uniform gravitational field.
- They can be different if the gravitational field varies across the object.
In practical terms, when designing anything from furniture to buildings, engineers need to consider both the CoM and CoG to ensure stability and prevent tipping over. In physics problems, knowing the CoM helps simplify complex systems to a single point, making calculations easier.
Position and Formulas of Centre of Mass of Some Homogeneous Bodies of Regular Shape
| Body Shape | Position of CoM |
|---|---|
| Uniform Hollow Sphere | At the center of the sphere |
| Uniform Solid Sphere | At the center of the sphere |
| Solid Hemisphere | At a height of \(\displaystyle \frac{3R}{8}\) above the flat face |
| Hemispherical Shell | At a height of \(\displaystyle \frac{R}{2} \) above the flat face |
| Uniform Circular Ring | At the center of the ring |
| Uniform Semi-Circular Ring | At a distance of \(\displaystyle \frac{4R}{3\pi} \) from the center along the diameter |
| Uniform Circular Disc | At the center of the disc |
| Uniform Semicircular Disc | At a distance of \(\displaystyle \frac{4R}{3\pi} \) from the center along the diameter |
| Rectangular Cubical Box | At the intersection of the diagonals (center) |
| Cone or Pyramid | At a height of \(\displaystyle \frac{H}{4} \) from the base (for a right cone or pyramid) |
For most of these bodies, if they have uniform density and regular shape, the CoM is located at the geometric center or along the axis of symmetry.
This table summarizes where you can find the CoM for these common shapes. Remember, the CoM is the point where you can balance the shape on the tip of a pencil without it tipping over.
Also Read: Collision
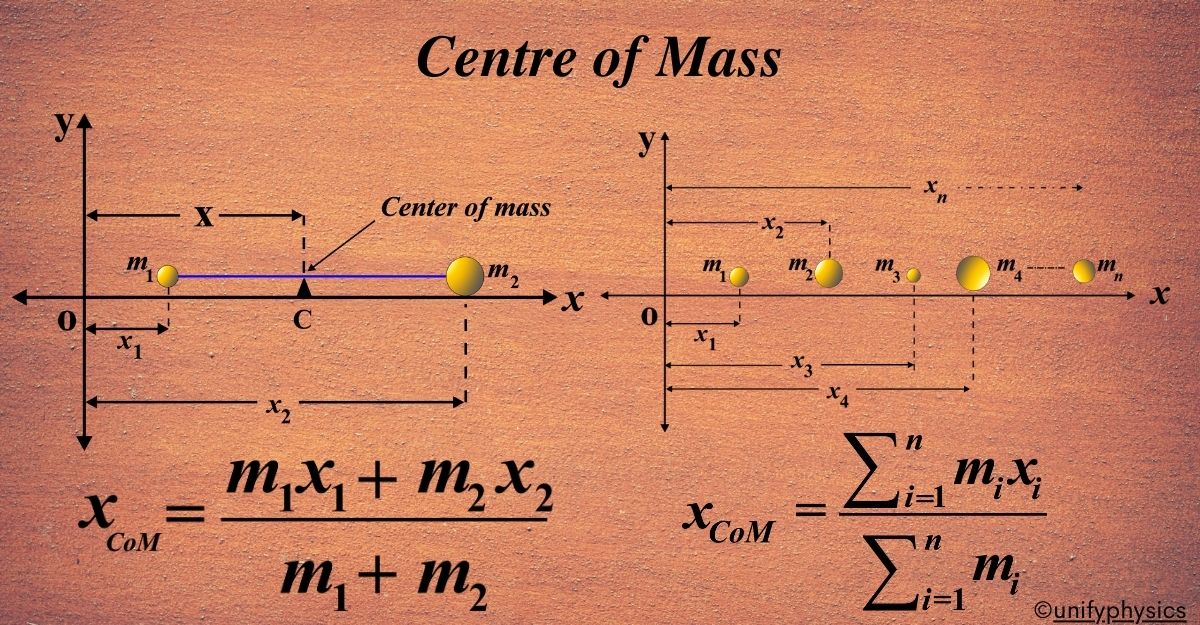
Centre of Mass of a System of Particles
The CoM of a system of particles is the weighted average of their positions, where the weights are their masses. To understand this, let’s consider a simple system of particles.

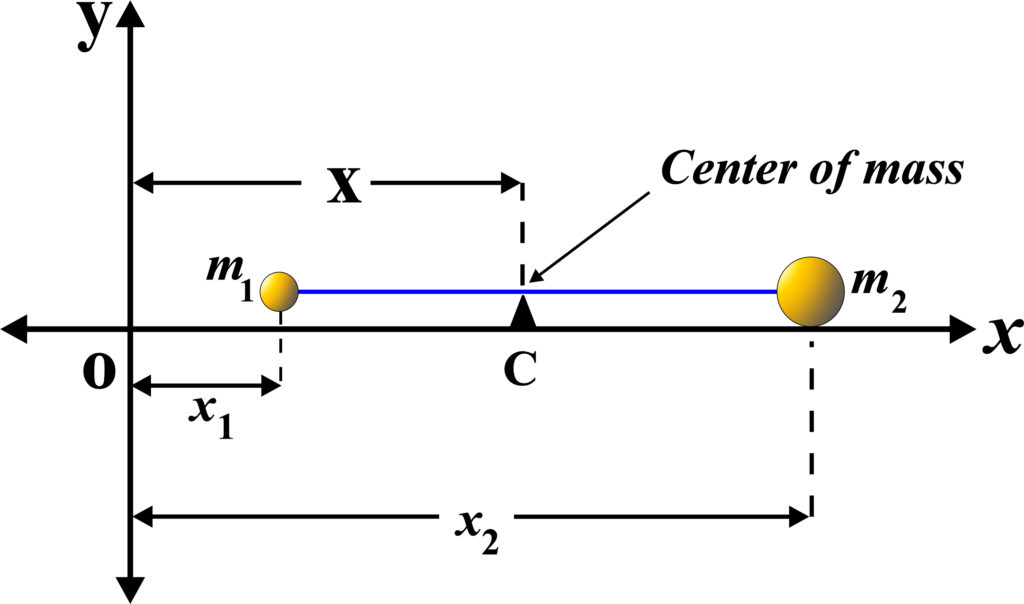
Think of a system with just two particles for simplicity. One particle has a mass of (m1) and is located at position (x1), and the other has a mass of (m2) and is at position (x2).
In Two Dimensions: The CoM, (xCoM), for these two particles can be found using the formula:
\(\displaystyle x_{\text{CoM}} = \frac{m_{1}x_{1} + m_{2}x_{2}}{m_{1} + m_{2}}\)
This formula is a weighted average of the positions of the particles, where the weights are their respective masses.
Generalizing to Many Particles: For a system with many particles, we generalize this formula. If we have (n) particles, each with a mass (mi) and position (xi), the CoM is given by:
\(\displaystyle x_{\text{CoM}} = \frac{\sum_{i=1}^{n} m_ix_i}{\sum_{i=1}^{n} m_i} \)
Here, ∑ denotes the sum of all particles in the system.
In Three Dimensions: In three dimensions, we have to consider the (x), (y), and (z) coordinates separately. So, we would have:
\(\displaystyle x_{\text{CoM}} = \frac{\sum m_ix_i}{M}, \quad y_{\text{CoM}} = \frac{\sum m_iy_i}{M}, \quad z_{\text{CoM}} = \frac{\sum m_iz_i}{M} \)
The CoM is important because it simplifies many physics problems. Instead of dealing with multiple particles moving in different ways, we can treat the whole system as if all its mass were concentrated at the CoM.
Example: Consider a school bus full of students. Each student is like a particle with mass, and the bus is the system. The CoM of the bus would be the point where you could balance it if it were possible to do so. It takes into account where each student (particle) is sitting and how much they weigh (mass).
Applications of the Centre of Mass
The CoM concept is crucial in mechanics, especially in the study of motion, stability, and balance. It’s used in designing vehicles, and buildings, and understanding celestial mechanics.
Solving Translational Motion Problems: By considering objects as point masses located at their CoM, we can simplify complex calculations involving linear momentum, kinetic energy, and collisions. This approach allows us to treat extended bodies as if all their mass were concentrated at a single point, making the math much easier.
Rocket Dynamics: The CoM is essential in analyzing the motion and stability of rockets. As the fuel burns, the mass distribution of a rocket changes, which in turn affects its CoM. Understanding this helps engineers design rockets that can be controlled and stabilized during flight.
Sports: In sports like gymnastics or diving, athletes must understand their CoM to perform complex maneuvers. They adjust their body position to control their rotation and balance, ensuring they land correctly.
Vehicle Design: The location of the CoM affects a vehicle’s stability. Designers aim to lower the CoM to reduce the risk of rollover and improve handling. This is why sports cars often have a lower CoM compared to SUVs.
Engineering and Construction: When building structures like bridges or buildings, engineers must calculate the CoM to ensure stability. The CoM affects how weight is distributed and how the structure will react to loads and forces.
Astronomy and Astrophysics: The CoM concept helps astronomers understand the orbits of planets and the behavior of galaxies. For example, the Earth-Moon system orbits around their common CoM, which is inside the Earth but not at its center.
Balance in Everyday Objects: From balancing a pencil on your finger to finding the best way to carry a heavy board, the CoM helps us understand how to achieve balance and avoid tipping over.
Physics Experiments: In the lab, experiments that involve pendulums, rotational motion, and equilibrium often require an understanding of the CoM to interpret results correctly.
These applications show that the CoM is more than just a theoretical concept; it’s a practical tool that helps us understand and predict the behavior of objects in our everyday world and complex scientific scenarios.
Solved Examples
Example 1:Determine the position of the center of mass of a uniform rod of length 2m and mass 4kg.
Solution: The center of mass of a uniform rod lies at its midpoint.
Given: Length of the rod (L) = 2m, Mass of the rod (M) = 4kg. Using the formula for the position of the center of mass of a uniform object,
\(\displaystyle \text{Center of mass (COM)} = \frac{L}{2} \)
\(\displaystyle\text{COM} = \frac{2}{2} \)
\(\displaystyle \text{COM} = 1m \)
Therefore, the center of mass of the uniform rod is located at a distance of 1 meter from either end.
Example 2: Determine the center of mass of a thin wire bent in the shape of a quarter circle with a radius of 3 meters, having linear mass density (λ(x) = 2x) kg/m.
Solution: To find the center of mass, we’ll need to integrate the mass elements along the length of the wire.
Mass of an element: \(\displaystyle dm = \lambda(x) \), dx
Total mass (M): \(\displaystyle \int dm = \int_0^3 2x \), \(\displaystyle dx = [x^2]_0^3 = 9 \) kg
Now, to find the x-coordinate of the center of mass (COM):
\(\displaystyle \text{COM}_x = \frac{1}{M} \int x \, dm = \frac{1}{9} \int_0^3 2x^2 \, dx = \frac{1}{9} \left[\frac{2}{3}x^3\right]_0^3 = \frac{18}{9} = 2 m\)
Therefore, the center of mass of the wire is located at (2, 2) meters.
Example 3: Find the center of mass of a system of three particles with masses 2kg, 3kg, and 4kg respectively, located at (1m, 0m), (2m, 0m), and (4m, 0m) respectively.
Solution: Center of Mass formula for a system of particles:
\(\displaystyle \text{COM}_x = \frac{m_1x_1 + m_2x_2 + m_3x_3}{m_1 + m_2 + m_3} \)
Given: \(\displaystyle m_1 = 2kg, m_2 = 3kg, m_3 = 4kg \) \(\displaystyle x_1 = 1m, x_2 = 2m, x_3 = 4m \)
\(\displaystyle \text{COM}_x = \frac{(2 \times 1) + (3 \times 2) + (4 \times 4)}{2 + 3 + 4} \)
\(\displaystyle \text{COM}_x = \frac{2 + 6 + 16}{9} = \frac{24}{9} = 2.67m \)
Therefore, the x-coordinate of the center of mass of the system of particles is 2.67 meters.
Example 4: Determine the center of mass of a triangular lamina with vertices at (0m, 0m), (2m, 0m), and (0m, 3m), having uniform mass distribution.
Solution: The center of mass of a triangle lies at the intersection of its medians, which divides each median into a 2:1 ratio.
Let’s consider the medians drawn from each vertex. The median from the vertex (0m, 0m) will coincide with the y-axis.
The median from the vertex (2m, 0m) will pass through (1m, 1.5m), and the median from the vertex (0m, 3m) will pass through (1m, 1.5m).
Therefore, the center of mass is at (1m, 1.5m).
Example 5: Find the center of mass of four particles with masses 1kg, 2kg, 3kg, and 4kg located at (1m, 2m, 3m), (2m, 3m, 4m), (3m, 4m, 5m), and (4m, 5m, 6m) respectively.
Solution: Center of Mass formula for a system of particles in 3D:
\(\displaystyle \text{COM}{x} = \frac{\sum{i=1}^{n} m_{i}x_{i}}{\sum_{i=1}^{n} m_{i}} \)
\(\displaystyle \text{COM}{y} = \frac{\sum{i=1}^{n} m_{i}y_{i}}{\sum_{i=1}^{n} m_{i}} \)
\(\displaystyle \text{COM}{z} = \frac{\sum{i=1}^{n} m_{i}z_{i}}{\sum_{i=1}^{n} m_{i}} \)
Given: \(\displaystyle m_1 = 1kg, m_2 = 2kg, m_3 = 3kg, m_4 = 4kg \)
\(\displaystyle x_1 = 1m, x_2 = 2m, x_3 = 3m, x_4 = 4m \)
\(\displaystyle y_1 = 2m, y_2 = 3m, y_3 = 4m, y_4 = 5m \)
\(\displaystyle z_1 = 3m, z_2 = 4m, z_3 = 5m, z_4 = 6m \)
\(\displaystyle \text{COM}{x} = \frac{(1 \times 1) + (2 \times 2) + (3 \times 3) + (4 \times 4)}{1 + 2 + 3 + 4} = \frac{30}{10} = 3m \)
\(\displaystyle \text{COM}{y} = \frac{(1 \times 2) + (2 \times 3) + (3 \times 4) + (4 \times 5)}{1 + 2 + 3 + 4} = \frac{40}{10} = 4m \)
\(\displaystyle \text{COM}_{z} = \frac{(1 \times 3) + (2 \times 4) + (3 \times 5) + (4 \times 6)}{1 + 2 + 3 + 4} = \frac{50}{10} = 5m \)
Therefore, the center of mass of the system of particles is located at (3m, 4m, 5m).
Example 6: Determine the center of mass of three particles with masses 1kg, 2kg, and 3kg respectively, located at (1m, 0m), (2m, 0m), and (3m, 0m) respectively, given that the mass distribution along the x-axis is ( m(x) = 2x ) kg.
Solution: To find the center of mass, we must integrate the mass elements along the x-axis.
Mass of an element: \(\displaystyle dm = m(x) \, dx = 2x \, dx \)
Total mass (M): \(\displaystyle \int dm = \int_1^3 2x \, dx = [x^2]_1^3 = 8 ) kg\)
Now, to find the x-coordinate of the center of mass (COM):
\(\displaystyle \text{COM}_x = \frac{1}{M} \int x \, dm = \frac{1}{8} \int_1^3 2x^2 \, dx = \frac{1}{8} \left[\frac{2}{3}x^3\right]_1^3 = \frac{16}{8} = 2 m\)
Therefore, the center of mass of the system of particles is located at (2, 0) meters.
FAQs
What is the center of mass, and why is it important in physics?
The center of mass of an object is the point at which the entire mass of the object can be considered to be concentrated. It is a crucial concept in physics because it simplifies the analysis of the motion of complex systems by allowing us to treat them as if all their mass were concentrated at a single point.
How is the center of mass of a body with continuous mass distribution determined?
For a body with continuous mass distribution, such as a uniform rod or a solid object, the center of mass can be calculated using calculus. It involves finding the weighted average of the positions of all the infinitesimal mass elements composing the object, with the weights being the mass of each element.
Can you explain how the center of mass of a system of particles is calculated?
The center of mass of a system of particles is calculated by taking the weighted average of the positions of all the particles in the system, with the weights being the mass of each particle. Mathematically, it is expressed as \(\displaystyle \vec{R}{\text{CM}} = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2 + \ldots + m_n \vec{r}_n}{m_1 + m_2 + \ldots + m_n} \).
How does the center of mass relate to the stability of an object?
The position of the center of mass is crucial for determining the stability of an object. An object is stable if its center of mass is located directly above its base of support. If the center of mass is outside the base of support, the object tends to topple over due to the gravitational force acting on it.
Can the center of mass be located outside the physical boundaries of an object?
Yes, the center of mass can be located outside the physical boundaries of an object, especially for irregularly shaped objects or systems with asymmetric mass distributions. For example, in a thin hoop or a crescent-shaped object, the center of mass may be located outside the object itself.
How is the concept of center of mass applied in engineering and design?
Engineers and designers use the concept of center of mass to ensure the stability and balance of structures, vehicles, and machines. By understanding the location of the center of mass, they can design objects with optimal weight distribution to minimize tipping, maximize performance, and enhance safety.
Can you provide an example illustrating the concept of center of mass in everyday life?
Imagine balancing a broomstick vertically on the palm of your hand. To keep the broomstick from falling over, you need to position your hand directly below the center of mass of the broomstick. If the center of mass is not directly above your hand, the broomstick will tip over. This demonstrates the importance of the center of mass in maintaining balance and stability.