The concepts of torque and angular momentum are rooted in the studies of rotational motion. Historically, scientists like Isaac Newton and James Clerk Maxwell contributed to our understanding of these concepts through their work on the laws of motion and electromagnetism.
The concept of torque, or the moment of force, has its roots in ancient times. It was Archimedes, a Greek mathematician, physicist, engineer, and inventor, who first studied the use of levers and articulated the principle of mechanical advantage. His famous quote, “Give me a lever and a place to stand and I will move the Earth,” reflects the fundamental idea of torque³.
The term “torque” itself comes from the Latin word torquēre, which means “to twist.” It was suggested by James Thomson, an engineer and physicist, and appeared in print in 1884³. This marked the formal introduction of the term in the scientific community.
Angular momentum, on the other hand, is a concept that evolved from the understanding of linear momentum. It’s the rotational equivalent of linear momentum and is a conserved quantity, meaning it remains constant in a closed system without external torques.
The classical representation of angular momentum for a point particle is a pseudovector \(\displaystyle \mathbf{r} \times \mathbf{p} \), which is the cross product of the particle’s position vector \(\displaystyle\mathbf{r}\) and its momentum vector \(\displaystyle \mathbf{p} \). This formulation is deeply rooted in Newtonian mechanics, where \(\displaystyle\mathbf{p} \) is the product of mass and velocity.
The conservation of angular momentum has profound implications in various fields, from engineering to astrophysics. It explains why bicycles remain stable while moving, why planets orbit stars, and even the formation of galaxies.
Both torque and angular momentum are central to the study of rotational dynamics. They are interconnected, with torque being the rate of change of angular momentum. This relationship is analogous to how force is the rate of change of linear momentum.
Moment of Force (Torque)
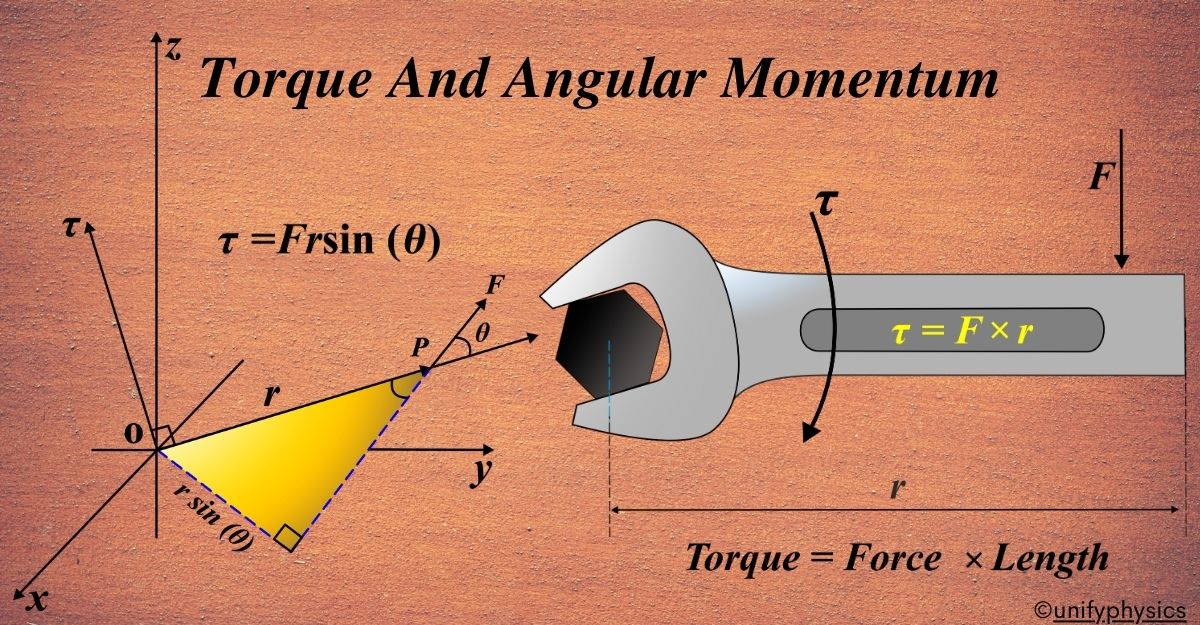
Torque, also known as the moment of force, is the rotational equivalent of force. It’s what causes objects to start rotating. The formula for torque (τ) is given by the cross product of the radius vector (r) and the force (F):
\(\displaystyle \tau = r \times F = rF \sin(\theta) \)
where (θ) is the angle between (r) and (F). Torque is a vector quantity, which means it has both magnitude and direction, and its SI unit is Newton-meter (Nm).
Imagine you’re trying to open a stubborn jar lid. You push down on the lid with your hand (that’s a force), but the lid won’t budge. Why? Because the force isn’t applied in the right way to rotate the lid open.
This is where torque (moment of force) comes in. Torque is the twisting power of a force. It’s what determines how easily you can rotate an object.
- Force: The push or pull you exert on the object.
- Distance: The distance between the point where you apply the force and the axis of rotation (the imaginary line around which the object rotates). The farther this distance is, the greater the torque. Imagine pushing on the edge of the lid compared to right next to the knob.
- Axis of rotation: The imaginary line around which the object rotates. The doorknob in our jar lid example.
The greater the force and the distance from the axis of rotation, the greater the torque.
So, going back to our jar lid, if you push down right next to the knob (a little distance), you won’t have much torque. But, if you push near the edge of the lid (farther distance), you’ll have more torque and the lid will be easier to open.
Torque is a vector, meaning it has a direction and a magnitude. The direction of the torque vector is perpendicular to the plane formed by the radius and the force, following the right-hand rule. If you curl the fingers of your right hand in the direction of rotation, your thumb points in the direction of the torque vector.
Think of using a wrench to tighten a bolt. The longer the wrench, the easier it is to turn the bolt because the lever arm (r) is longer, increasing the torque. Also, applying force at a 90-degree angle to the wrench gives you the maximum torque because \(\displaystyle \sin(90^\circ) = 1 \).
The angle is crucial because it determines how effectively the force contributes to rotation. If you push straight down on a seesaw, you won’t make it tilt, but if you push sideways, you’ll create rotation. That’s why we use the sine of the angle in our torque formula.
Example 1: Imagine you’re pushing on a door at a point P. The door’s hinge is at the origin O. The position vector (r) is an arrow from O to P, where you’re pushing. The force (F) is what you’re applying at P to open the door.

The torque (τ) is the vector product (also known as the cross product) of (r) and (F):
\(\displaystyle \tau = r \times F \)
The magnitude of torque is given by:
\(\displaystyle \tau = rF \sin(\theta) \)
- (r) is the length of the position vector (the distance from O to P).
- (F) is the magnitude of the force you’re applying.
- (θ) is the angle between the position vector (r) and the force (F).
The direction of torque is perpendicular to the plane formed by (r) and (F), following the right-hand rule. If you curl the fingers of your right hand from (r) to (F), your thumb points in the direction of (τ).
- Lever Arm: The distance (r) is also called the lever arm. It’s like the length of the wrench you use to tighten a bolt.
- Angle (θ): The angle is crucial because it tells us how effectively the force contributes to the rotation. If (θ) is 0 or 180 degrees, the force doesn’t cause rotation, hence no torque.
- Right-Hand Rule: This rule helps you figure out the direction of the torque vector. It’s a handy way to remember which way things will spin.
When you use a wrench, you’re applying torque to a bolt. The further from the bolt you apply the force (larger (r), and the more perpendicular the force is to the wrench (larger \(\displaystyle \sin(\theta) \)), the more torque you have, and the easier it is to turn the bolt.
Example 2: Imagine you have a nut and bolt that need tightening. You grab a double-ended spanner, which is a tool with two arms of different lengths. One arm is short, and the other arm is longer.
Now, let’s say you use the short arm of the spanner to tighten the nut. You apply the same force to both arms of the spanner, but because the short arm is closer to the bolt’s axis (the point where it rotates), it’s harder to turn. This is because the distance from the axis to where you apply the force is shorter.
On the other hand, if you use the long arm of the spanner, even though you’re applying the same force as before, it’s much easier to turn the bolt. Why? Because the longer arm increases the distance from the axis to where you apply the force, making it more effective in turning the bolt.
This difference in effectiveness is what we call torque or moment of force. It’s a measure of how effectively a force can make something rotate around a pivot point. In this case, the pivot point is the bolt’s axis, and the force is the one you apply using the spanner.
So, when you’re tightening a nut or bolt with a spanner, you’re not just applying force; you’re also leveraging the distance between the force you apply and the pivot point to make the job easier. The longer the lever arm (distance), the greater the torque, and the easier it is to turn the bolt.
By understanding torque, you can understand how to apply forces effectively to rotate objects, from opening jars to using levers and wrenches.
Also Read: Rigid Body
Angular Momentum of Particle
Angular momentum is to rotational motion and linear momentum is to linear motion. It’s a measure of an object’s tendency to continue rotating.
Think of angular momentum as the ‘spin’ version of momentum. Just like how a moving car has momentum, a spinning wheel has angular momentum.
Angular momentum is a measure of how much rotation an object has and how difficult it is to stop that rotation. It’s a vector quantity, which means it has both a magnitude (how much) and a direction (which way).
The angular momentum (L) of a particle is given by the cross product of its position vector (r) and its linear momentum (p):
\(\displaystyle L = r \times p \)
- Position Vector (r): This is a straight line drawn from the point of rotation to where the force is applied.
- Linear Momentum (p): This is the product of the mass (m) of the particle and its velocity (v). It represents how much motion the particle has in a straight line.
- Cross Product: This isn’t just simple multiplication. It’s a special way to multiply two vectors to get another vector that’s perpendicular to both.
The right-hand rule determines the direction of angular momentum. If you point your fingers in the direction of (r ) and curl them toward (p), your thumb points in the direction of (L ).
Let’s derive the expression for the Angular Momentum of a Particle. Angular momentum (L) is a measure of how much rotation a particle has. It’s like the spinning version of straight-line momentum. For a single particle, angular momentum is the cross product of its position vector (r) and its linear momentum (p):
\(\displaystyle L = r \times p \)
Now, let’s see how torque ( \tau), which is the moment of force, relates to angular momentum. We know that torque is what causes an object to start rotating, and it’s the rotational equivalent of force.
To find the relationship between torque and angular momentum, we differentiate the angular momentum with respect to time (t).
Start with the definition of angular momentum:
\(\displaystyle L = r \times p \)
Differentiate both sides of the above equation with respect to time:
\(\displaystyle \frac{dL}{dt} = \frac{d}{dt} (r \times p) \)
Apply the product rule for differentiation to the right side, which gives us two terms. However, since (p = mv) (mass times velocity), and (v) is the derivative of (r) with respect to time, the term ( v × v ) will be zero. So we’re left with:
\(\displaystyle \frac{dL}{dt} = r \times \frac{dp}{dt} \)
Recognize that \(\displaystyle\frac{dp}{dt} \) is just the force (F) acting on the particle. So we can rewrite the equation as:
\(\displaystyle \frac{dL}{dt} = r \times F \)
And since (r × F) is the definition of torque, we have our final relationship:
\(\displaystyle \tau = \frac{dL}{dt} \)
This equation tells us that torque is the rate of change of angular momentum. It’s a powerful concept because it connects rotational motion to Newton’s second law of motion, which relates force to the rate of change of linear momentum.
In simpler terms, if you apply a force to a particle at some distance from a pivot point, you’ll create torque. This torque changes the particle’s angular momentum, causing it to rotate faster or slower depending on the direction of the force.
Torque and Angular Momentum for a System of Particles
When we talk about a system of particles, we look at more than one particle, each possibly experiencing different forces. Torque in this context is the measure of how these forces cause the entire system to rotate.
For each particle, we calculate the torque individually, just like we would for a single particle:
\(\displaystyle \tau_i = r_i \times F_i \)
where (τi) is the torque on the (ith) particle, (ri) is the position vector of the (ith) particle, and (Fi) is the force acting on it.
First, imagine you have a group of particles, each spinning around. Each particle has its angular momentum based on its mass, velocity, and distance from the point of rotation. To understand the entire system’s rotation, we need to look at all these particles together.
For one particle, angular momentum (L) is given by:
\(\displaystyle L = r \times p \)
For the whole system, the total angular momentum (Ltotal) is the vector sum of the angular momenta of all the individual particles:
\(\displaystyle L_{total} = \sum L_i \)
where (Li) is the angular momentum of the (ith) particle.
Torque (τ) is related to angular momentum in a similar way that force is related to linear momentum. It’s the rotational ‘push’ that can change the angular momentum of a system.
Now, let’s derive the relationship between torque and the total angular momentum for our system of particles. Start with the definition of torque for one particle:
\(\displaystyle \tau_i = r_i \times F_i \)
The total torque on the system is the sum of the torques on all particles:
\(\displaystyle \tau_{total} = \sum \tau_i \)
From Newton’s second law, we know that the force is the rate of change of linear momentum (p):
\(\displaystyle F_i = \frac{dp_i}{dt} \)
Substituting this into our torque equation gives us:
\(\displaystyle \tau_{total} = \sum (r_i \times \frac{dp_i}{dt}) \)
But we also know that the rate of change of angular momentum for one particle is:
\(\displaystyle \frac{dL_i}{dt} = r_i \times \frac{dp_i}{dt} \)
So, the rate of change of the total angular momentum for the system is:
\(\displaystyle\frac{dL_{total}}{dt} = \sum \frac{dL_i}{dt} = \sum (r_i \times \frac{dp_i}{dt}) \)
Therefore, we can say that the total torque is equal to the rate of change of the total angular momentum of the system:
\(\displaystyle \tau_{total} = \frac{dL_{total}}{dt} \)
This means if you add up all the torques acting on all the particles and calculate how this sum changes over time, you get the rate at which the total angular momentum of the system changes.
Conservation of Angular Momentum:
When the Conservation of Angular Momentum applies, it means that no external torques are acting on the system, or the net external torque is zero. This leads to the total angular momentum of the system being constant over time.
The expression for the rate of change of the total angular momentum of the system, which we derived earlier, is:
\(\displaystyle \tau_{total} = \frac{dL_{total}}{dt} \)
Under the conservation of angular momentum, since the net external torque (τtotal) is zero, the equation simplifies to:
\(\displaystyle 0 = \frac{dL_{total}}{dt} \)
This implies that the total angular momentum (Ltotal) does not change with time, so we can say:
\(\displaystyle L_{total} = \text{constant} \)
The time rate of the total angular momentum of a system of particles about a point is equal to the sum of the external torques (i.e. the torques due to external forces) acting on the system taken about the same point.
In a closed system where no external torques act, the total angular momentum remains constant. This is the principle of conservation of angular momentum. It’s like having a set amount of ‘spin’ that can’t be lost or gained, only transferred within the system.
In other words, the total angular momentum before any event (like a collision or explosion) is equal to the total angular momentum after the event, as long as no external forces interfere.
Solved Examples
Example 1:Calculate the torque exerted on a wrench handle of length 0.3 meters when a force of 20 Newtons is applied perpendicular to it at a distance of 0.15 meters from the pivot point.
Solution: Given; (r = 0.15 m), (F = 20 N)
Torque (τ) is given by the formula \(\displaystyle \tau = r \times F \) . Where (r) is the lever arm or distance from the pivot point to the point of application of force.
\(\displaystyle \tau = 0.15 \, m \times 20 \, N = 3 \, Nm \)
Therefore, the torque exerted on the wrench handle is ( 3 Nm).
Example 2: Calculate the angular momentum of a disc with a mass of 2 kg and a radius of 0.5 meters rotating at an angular velocity of 10 radians per second.
Solution: Given; (m = 2 kg), (r = 0.5 m), (ω = 10 rad/s)
Angular momentum (L) is given by the formula \(\displaystyle L = I \times \omega \).
Moment of inertia (I) for a disc is \(\displaystyle I = \frac{1}{2} m r^2 \)
\(\displaystyle I = \frac{1}{2} \times 2 \, kg \times (0.5 \, m)^2 = 0.5 \, kg \cdot m^2 \)
\(\displaystyle L = 0.5 \, kg \cdot m^2 \times 10 \, rad/s = 5 \, kg \cdot m^2/s \)
Therefore, the angular momentum of the disc is ( 5 \, kg \cdot m^2/s ).
Example 3: Calculate the torque exerted by a force of 30 Newtons acting on a door at an angle of 60 degrees to the door’s surface. The distance from the hinge to the point of force application is 0.4 meters.
Solution: Given; (F = 30 N), (θ = 60∘), ( r = 0.4 m)
To find the component of the force perpendicular to the door’s surface, we use the formula
\(\displaystyle F_{\perp} = F \sin \theta \)
\(\displaystyle F_{\perp} = 30 \, N \times \sin(60^\circ) = 30 \, N \times \frac{\sqrt{3}}{2} = 15 \sqrt{3} \, N \)
Torque (τ) is given by the formula \(\displaystyle\tau = r \times F_{\perp} \)
\(\displaystyle \tau = 0.4 \, m \times 15 \sqrt{3} \, N = 6 \sqrt{3} \, Nm \)
Therefore, the torque exerted on the door is ( 6 \sqrt{3} \, Nm ).
Example 4: A skater with a moment of inertia of \(\displaystyle 3 \, kg \cdot m^2 \) is initially rotating with an angular velocity of \(\displaystyle 4 \, rad/s \). She then pulls her arms inward, reducing her moment of inertia to \(\displaystyle 2 \, kg \cdot m^2 \). Calculate her final angular velocity assuming no external torques act on her.
Solution: Initial angular momentum (Li) equals final angular momentum (Lf) due to the conservation of angular momentum.
\(\displaystyle( L_i = L_f )\)
\(\displaystyle I_i \omega_i = I_f \omega_f )\)
\(\displaystyle (3 \, kg \cdot m^2) \times (4 \, rad/s) = (2 \, kg \cdot m^2) \times \omega_f \)
\(\displaystyle \omega_f = \frac{(3 \, kg \cdot m^2) \times (4 \, rad/s)}{2 \, kg \cdot m^2} = 6 \, rad/s \)
Therefore, her final angular velocity is ( 6 rad/s).
Example 5: A force of 50 Newtons is applied tangentially to a wheel with a radius of 0.2 meters. Calculate the torque produced by the force if it acts at a distance of 0.15 meters from the center of the wheel.
Solution: Given: (F = 50 N), (r = 0.15 m )
Torque (τ) is given by the formula \(\displaystyle\tau = r \times F \)
\(\displaystyle \tau = 0.15 \, m \times 50 \, N = 7.5 \, Nm \)
Therefore, the torque produced by the force is ( 7.5 Nm ).
Example 6: Two ice skaters of masses 60 kg and 40 kg respectively are initially at rest on frictionless ice. The skater with a mass of 60 kg pushes the skater with a mass of 40 kg away with a force that lasts for 0.5 seconds. Calculate the angular velocity of the skaters after the push, assuming they remain in contact and there are no external torques.
Solution: The angular momentum of the system before the push is zero since the skaters are at rest. After the push, the system’s total angular momentum is conserved.
The impulse (J) exerted by the skater with a mass of 60 kg on the skater with a mass of 40 kg is given by \(\displaystyle J = F \times \Delta t \)
\(\displaystyle J = 50 \, N \times 0.5 \, s = 25 \, Ns \)
According to the conservation of angular momentum, \(\displaystyle I_1 \omega_1 = I_2 \omega_2 \) .
Let (I) be the moment of inertia of the system.
\(\displaystyle I \omega_1 = I \omega_2 \)
Since (I) is constant, \(\displaystyle\omega_1 = \omega_2 \).
Therefore, the angular velocity of both skaters after the push is the same as before the push, and it remains zero.
FAQs
What is torque in physics, and how is it different from force?
Torque is a measure of the rotational force applied to an object, causing it to rotate around an axis. While force causes linear motion, torque causes rotational motion. Mathematically, torque is defined as the product of the force applied and the distance from the axis of rotation to the point where the force is applied, often represented as 𝜏=𝑟⃗×𝐹⃗.
Can you explain how torque affects the rotational motion of an object?
Torque produces angular acceleration in an object, causing it to rotate around an axis. The magnitude of the torque depends on the magnitude of the force applied, the distance from the axis of rotation (lever arm), and the angle between the force and the lever arm. The direction of the torque is perpendicular to both the force and the lever arm.
What factors affect the magnitude of torque produced by a force?
The magnitude of torque produced by a force depends on the magnitude of the force, the distance from the axis of rotation to the point of application of the force (lever arm), and the angle between the force and the lever arm. Increasing any of these factors will increase the torque.
How is torque related to angular momentum?
Torque is the rate of change of angular momentum. When a torque is applied to an object, it causes a change in the object’s angular momentum, resulting in rotational motion. Mathematically, torque is equal to the rate of change of angular momentum, \(\displaystyle \tau = \frac{dL}{dt} \).
Can you provide examples of everyday objects where torque is essential?
Examples include door handles, wrenches, and steering wheels. When you push or pull a door handle, apply force to a wrench, or turn a steering wheel, you are applying torque to produce rotational motion around an axis.
How is torque utilized in mechanical engineering and construction?
In mechanical engineering and construction, torque is essential for designing and analyzing various mechanisms, such as gears, pulleys, and machinery. Engineers use torque calculations to ensure that machines can perform tasks efficiently and safely, taking into account factors such as load, friction, and mechanical stress.
What are the practical implications of understanding torque and angular momentum in sports and athletics?
Understanding torque and angular momentum is crucial in sports and athletics, particularly in activities involving throwing, hitting, or rotating motions. Athletes use torque to generate power and speed in movements like throwing a baseball or swinging a golf club, while coaches and trainers use biomechanical principles to optimize technique and prevent injury.