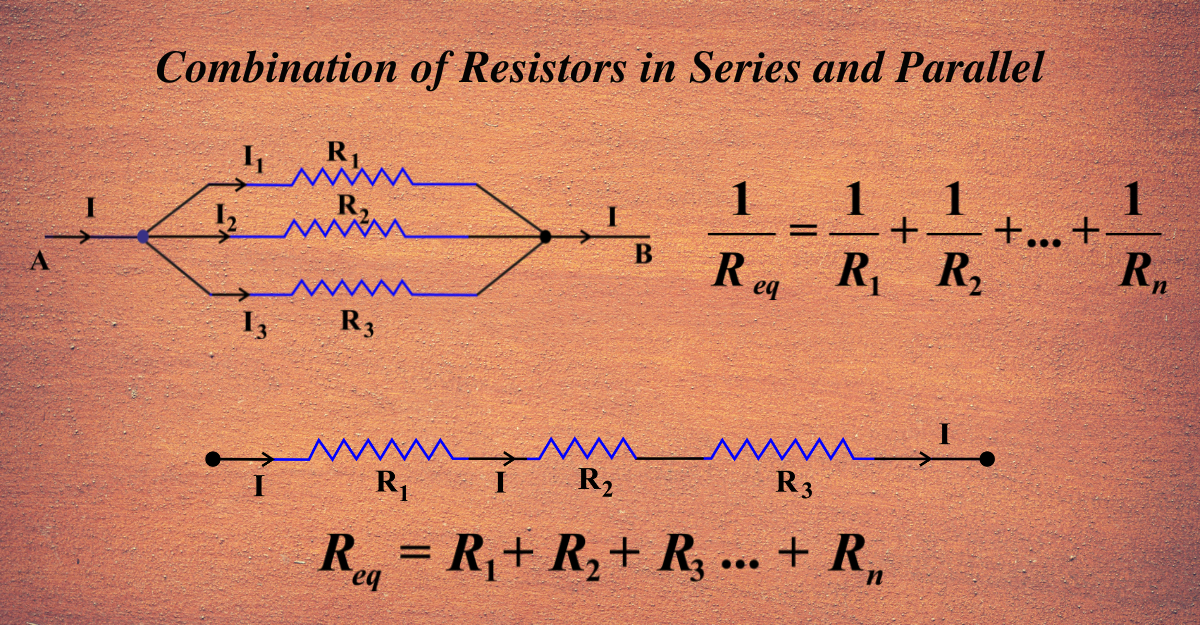
Combination of Resistors in Series
The combination of resistors in series is a way of connecting two or more resistors in such a way that the same current flows through all of them. The resistors are arranged one after another, and the ends of the first resistor are connected to the ends of the second resistor, and so on. The total resistance of the series combination is the sum of the individual resistances.
To derive the formula for the total resistance of the series combination, we can use the concept of equivalent resistance. The equivalent resistance of a circuit is the single resistance that can replace the entire circuit without changing the current or the voltage. For a series combination, the equivalent resistance is equal to the total resistance.

Let us consider a series combination of n resistors, R1, R2, …, Rn, connected to a battery of voltage V. The current flowing through the circuit is I. The diagram below shows the circuit and its equivalent resistance.
According to Ohm’s law, the voltage across each resistor is equal to the product of the current and the resistance. Therefore, we can write:
\(\displaystyle V_1 = I R_1\)
\(\displaystyle V_2 = I R_2\)
\(\displaystyle…\)
\(\displaystyle V_n = I R_n\)
The total voltage across the series combination is equal to the sum of the individual voltages. Therefore, we can write:
\(\displaystyle V = V_1 + V_2 + … + V_n\)
Substituting the expressions for the individual voltages, we get:
\(\displaystyle V = I R_1 + I R_2 + … + I R_n\)
Factoring out the current, we get:
\(\displaystyle V = I (R_1 + R_2 + … + R_n)\)
But we also know that the voltage across the series combination is equal to the product of the current and the equivalent resistance. Therefore, we can write:
\(\displaystyle V = I R_{eq}\)
Comparing the two expressions for the voltage, we get:
\(\displaystyle I (R_1 + R_2 + … + R_n) = I R_{eq}\)
Dividing both sides by the current, we get:
\(\displaystyle R_1 + R_2 + … + R_n = R_{eq}\)
This is the formula for the total resistance of the series combination. It shows that the total resistance is the sum of the individual resistances.
For example, if we have three resistors of 10 Ω, 20 Ω, and 30 Ω connected in series, the total resistance is:
\(\displaystyle R_{eq} = R_1 + R_2 + R_3\)
\(\displaystyle R_{eq} = 10 Ω + 20 Ω + 30 Ω\)
\(\displaystyle R_{eq} = 60 Ω\)
Combination of Resistors in Parallel
The combination of resistors in parallel is a way of connecting two or more resistors in such a way that the same voltage is applied across all of them. The resistors are arranged side by side, and the ends of each resistor are connected to the same points. The total resistance of the parallel combination is less than the smallest individual resistance.
To derive the formula for the total resistance of the parallel combination, we can use the concept of equivalent resistance. The equivalent resistance of a circuit is the single resistance that can replace the entire circuit without changing the current or the voltage. For a parallel combination, the equivalent resistance is equal to the total resistance.

Let us consider a parallel combination of n resistors, \(\displaystyle R_1, R_2, …, R_n\), connected to a battery of voltage V. The current flowing through the circuit is I. The diagram below shows the circuit and its equivalent resistance.
According to Ohm’s law, the current through each resistor is equal to the ratio of the voltage and the resistance. Therefore, we can write:
\(\displaystyle I_1 = \frac{V}{R_1}\)
\(\displaystyle I_2 = \frac{V}{R_2}\)
\(\displaystyle…\)
\(\displaystyle I_n = \frac{V}{R_n}\)
The total current through the parallel combination is equal to the sum of the individual currents. Therefore, we can write:
\(\displaystyle I = I_1 + I_2 + … + I_n\)
Substituting the expressions for the individual currents, we get:
\(\displaystyle I = \frac{V}{R_1} + \frac{V}{R_2} + … + \frac{V}{R_n}\)
Factoring out the voltage, we get:
\(\displaystyle I = V (\frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n})\)
But we also know that the current through the parallel combination is equal to the ratio of the voltage and the equivalent resistance. Therefore, we can write:
\(\displaystyle I = \frac{V}{R_{eq}}\)
Comparing the two expressions for the current, we get:
\(\displaystyle V (\frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}) = \frac{V}{R_{eq}}\)
Dividing both sides by the voltage, we get:
\(\displaystyle \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n} = \frac{1}{R_{eq}}\)
This is the formula for the total resistance of the parallel combination. It shows that the inverse of the total resistance is the sum of the inverses of the individual resistances.
For example, if we have three resistors of 10 Ω, 20 Ω, and 30 Ω connected in parallel, the total resistance is:
\(\displaystyle\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}\)
\(\displaystyle \frac{1}{R_{eq}} = \frac{1}{10 Ω} + \frac{1}{20 Ω} + \frac{1}{30 Ω}\)
\(\displaystyle\frac{1}{R_{eq}} = 0.15 Ω^{-1}\)
\(\displaystyle R_{eq} = \frac{1}{0.15 Ω^{-1}}\)
\(\displaystyle R_{eq} = 6.67 Ω\)