Equilibrium Of A Rigid Body

The concept of equilibrium is fundamental in physics and has been studied for centuries. It’s all about balance and the absence of net forces or motion.

The earliest ideas of equilibrium can be traced back to the works of ancient Greek philosophers. They observed that objects tend to come to a rest state, a form of equilibrium, which they attributed to their natural place in the universe.

The Renaissance brought a more scientific approach to the study of motion and forces. Galileo Galilei, for instance, studied the conditions under which objects remain at rest or move with a constant velocity—key ideas in understanding equilibrium.

The real breakthrough came with Sir Isaac Newton in the 17th century. His First Law of Motion, also known as the Law of Inertia, states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. This law laid the foundation for the concept of translational equilibrium.

Following Newton, scientists developed the field of statics, which deals with the analysis of loads (force, moment) on physical systems in static equilibrium—that is, in a state where the system is at rest or its center of mass moves at a constant velocity.

In the 19th century, engineers like Léon Foucault and mathematicians like Louis Poinsot made significant contributions to the understanding of rotational equilibrium, where an object is in a state where it is not rotating or is rotating at a constant rate.

Today, the principles of equilibrium are applied in various fields, from engineering structures that must remain stable to understanding the orbits of celestial bodies. The concept is also crucial in the design of machines and in the study of materials.

What is the Equilibrium

Imagine you’re holding a meter stick perfectly balanced on your finger. That’s equilibrium! In physics terms, equilibrium of a rigid body means the stick isn’t moving or tilting – it’s staying still. But why?

Here’s the key: there are two things we need to consider for a rigid body (an object that doesn’t bend or deform) to be in equilibrium – no overall movement (translational equilibrium) and no spinning (rotational equilibrium).

Think about the meter stick again. If you push one end down, it will tilt. That tilt is because the forces acting on it (your push and gravity) aren’t balanced. But for equilibrium, we want the total force acting on the stick to be zero. That means all the pushes and pulls acting on it must cancel each other out.

Now, let’s talk about spinning. Imagine a weight hanging on a string. If you nudge the weight slightly, it will swing back and forth. That’s because the string doesn’t prevent rotation. But for equilibrium, we want the meter stick not to rotate around your finger. To achieve this, the torques (turning effects) acting on the stick must also cancel each other out. Torque depends on both the force and its distance from the rotation point (your finger in this case).

In physics, when we talk about a rigid body, we mean an object that doesn’t bend or change shape no matter what forces are acting on it. So, a rigid body could be something like a metal rod, a wooden plank, or even a toy car.

Condition For Equilibrium

Think of a tightrope walker balancing on a rope. They’re not falling or speeding up in any direction. That’s because they’re in equilibrium. Now, let’s see what it takes for anything, like our tightrope walker, to be in this balanced state.

First Condition: No Net Force

The first thing needed for equilibrium is no net force. This means all the forces pushing or pulling on an object need to cancel out. It’s like having two friends pushing you on a swing with the same strength from opposite sides. You wouldn’t move because the forces are balanced. In physics, we write this as:

\(\displaystyle \sum \vec{F} = 0 \)

Second Condition: No Net Torque

The second thing is no net torque. A torque is a twist or turn that can make something rotate. For equilibrium, all the torques also need to cancel out. Imagine you and a friend are sitting on opposite ends of a seesaw, and you’re both the same weight and the same distance from the center. The seesaw wouldn’t tilt because the torques are balanced. We write this condition as:

\(\displaystyle \sum \tau = 0 \)

When both these conditions are met, an object is in equilibrium. It won’t start moving or spinning on its own. It’ll either stay still or keep moving at the same speed and in the same direction without changing.

So, for our tightrope walkers to stay perfectly balanced, they need to make sure they’re not leaning too much one way or the other (no net force) and not starting to spin (no net torque). It’s all about keeping everything in check so that there’s no unexpected movement.

In simple terms, a rigid body is in equilibrium when it’s either sitting still or moving in a straight line at a constant speed, and it’s not spinning or starting to spin. It’s all about balance—no extra pushes, pulls, or twists that would cause it to start moving or stop.

The equilibrium of a rigid body refers to a state where the body experiences no net force or net torque, resulting in neither translation nor rotation. This concept can be illustrated using the example of a man on a teeter-totter (also known as a seesaw) attempting to balance.

Example: Imagine a teeter-totter with a fulcrum at the center and a man seated on one end. For the teeter-totter to be in equilibrium, two conditions must be met: force equilibrium and torque equilibrium.

Force Equilibrium: The man exerts a downward force due to his weight, which acts vertically downward. According to Newton’s third law of motion, the ground exerts an equal and opposite force upward on the man. Similarly, the teeter-totter exerts a reaction force upward on the man. These forces form an action-reaction pair and balance each other out, resulting in force equilibrium. The sum of the vertical forces is zero.

Torque Equilibrium: In addition to the vertical forces, there are torques acting on the teeter-totter. The man’s weight creates a torque about the fulcrum, which tends to rotate the teeter-totter in a clockwise or counterclockwise direction, depending on the man’s position relative to the fulcrum. To achieve torque equilibrium and prevent rotation, the torque produced by the man’s weight must be balanced by an opposing torque. This opposing torque is provided by the force exerted by the man’s feet pushing against the ground, which creates a counteracting torque about the fulcrum. By adjusting his position on the teeter-totter, the man can balance the torques and keep the teeter-totter in rotational equilibrium.

The equilibrium of the teeter-totter is achieved when the downward force exerted by the man’s weight is balanced by the reaction force from the ground, and the torque created by the man’s weight is counteracted by the torque produced by the force from his feet pushing against the ground. This example demonstrates how the principles of force and torque equilibrium apply to a real-world situation involving a rigid body.

Types of Equilibrium

Translational Equilibrium

Translational equilibrium occurs when the sum of all forces acting on a body is zero, leading to no change in its linear motion.

Imagine you’re playing tug-of-war. Your team is pulling on one side, and the other team is pulling just as hard on the other side. If neither team is winning, and the rope isn’t moving, you’re experiencing translational equilibrium.

In physics, translational equilibrium happens when all the forces acting on an object add up to zero. This means the object won’t speed up, slow down, or change direction—it’ll either stay still or keep moving straight at the same speed.

Net Force is Zero: For an object to be in translational equilibrium, the total (or net) force acting on it must be zero. We can write this using a fancy physics equation:

\(\displaystyle \sum \vec{F} = 0 \)

This means if you add up all the forces (like pushes and pulls) acting on an object, they should cancel each other out.

No Acceleration: Because the net force is zero, the object won’t accelerate. Remember, acceleration means changing speed or direction. So, if an object is in translational equilibrium, it’s either not moving at all or moving at a constant speed in a straight line.

Example:

• Stationary Object: A book resting on a table is in translational equilibrium. Gravity pulls it down, but the table pushes it up with an equal force, so the book doesn’t move.
• Moving Vehicle: A car cruising at a steady speed on a straight road is also in translational equilibrium. The engine’s push forward is balanced by air resistance and friction pushing back, so the car keeps moving at the same speed.

Rotational Equilibrium

Rotational equilibrium occurs when the sum of all torques acting on a body is zero, leading to no change in its rotational motion.

Think of a spinning top. When it’s spinning smoothly and doesn’t speed up or slow down, it’s in rotational equilibrium.

In physics, rotational equilibrium is about an object’s rotation. It means that the object is either not rotating at all or rotating at a constant speed. It’s not speeding up (accelerating) or slowing down (decelerating).

Net Torque is Zero: For an object to be in rotational equilibrium, the total (or net) torque acting on it must be zero. Torque is like a force that makes things spin or rotate. We can write this condition as:

\(\displaystyle \sum \vec{\tau} = 0 \)

This means if you add up all the torques (the twists and turns) acting on an object, they should cancel each other out.

No Angular Acceleration: Because the net torque is zero, the object won’t have any angular acceleration. Angular acceleration is how fast something speeds up or slows down when it’s spinning. So, if an object is in rotational equilibrium, it’s either not spinning at all or spinning at a constant rate.

Example:

• Ceiling Fan: A ceiling fan running at a steady speed is in rotational equilibrium. The motor applies a torque to spin the fan, and the air resistance applies an opposite torque. When these torques are balanced, the fan spins at a constant rate without speeding up or slowing down.
• Balanced Wheel: A bicycle wheel spinning smoothly as you ride is another example. The forces acting on the wheel are balanced, so it keeps spinning at the same rate unless you pedal harder or hit the brakes.

Partial Equilibrium

Partial equilibrium refers to the condition where only a part of the system is in equilibrium, while other parts may not be.

Imagine you’re watching a movie where the main character is trying to balance on a tightrope. They’re not falling off, but they’re also not perfectly still—they’re moving a little bit to keep their balance. This is similar to partial equilibrium.

Partial Equilibrium is a state where a rigid body is in equilibrium in one way but not necessarily in another. It means the body might be in translational equilibrium (not speeding up or slowing down in a straight line) but not in rotational equilibrium (it might be spinning), or vice versa.

It’s called ‘partial’ because the body isn’t in complete equilibrium. It’s only partway there—like having one foot on stable ground and the other in the air. The body is balanced in one aspect of its motion but not in all aspects.

• One Condition Met: For partial equilibrium, only one of the two main conditions for full equilibrium needs to be met. Either the net force is zero (translational equilibrium) or the net torque is zero (rotational equilibrium), but not necessarily both.
• Possible Movement: Because it’s only partial, the body might still move or rotate in some way. It’s like a spinning top that’s not wobbling (rotational equilibrium) but is still moving across the table (not in translational equilibrium).

Example:

• A Spinning Wheel: A bicycle wheel that’s spinning in place is in rotational equilibrium but not in translational equilibrium because it’s not moving forward.

So, partial equilibrium is like being halfway to a complete standstill. It’s a useful concept when analyzing systems where some parts are stable, and others are still in motion.

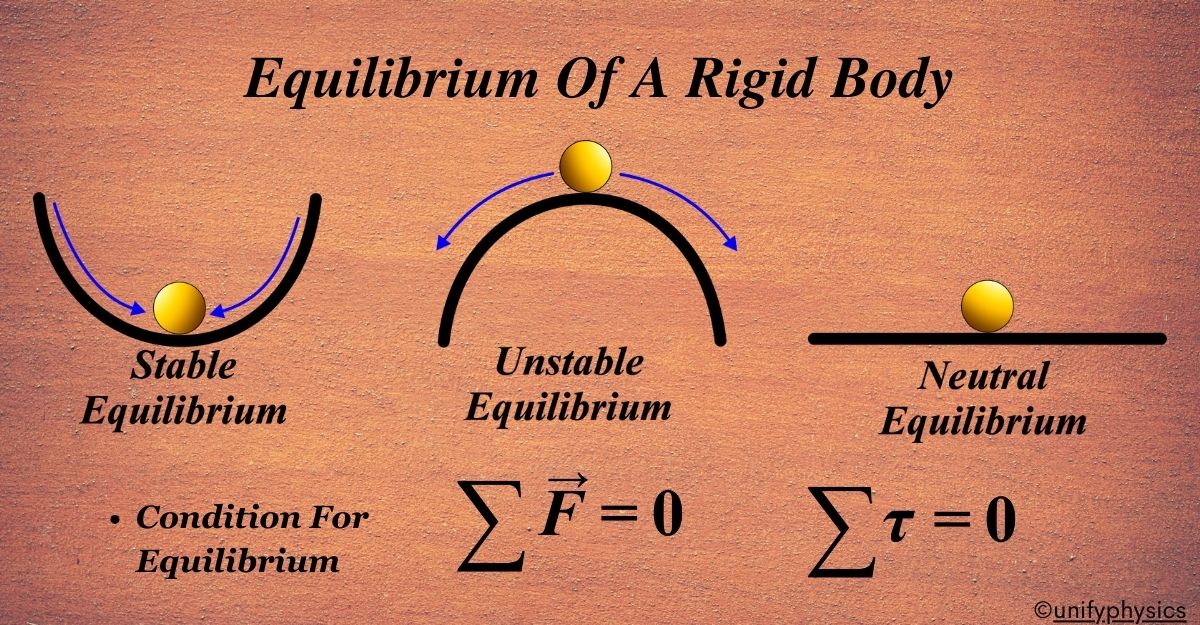
Stability of Equilibrium

Stable Equilibrium

If displaced, the body tends to return to its original position. Imagine you’re sitting in the middle of a bowl-shaped valley. No matter which way you lean, you’ll always roll back to the center. This is like being in a stable equilibrium.

In physics, an object is in stable equilibrium if, after a slight push or nudge, it returns to its original position. Here’s why:

• Restoring Force: When you push an object in stable equilibrium, it experiences a force that pushes it back toward where it started. It’s like a marble in a bowl; if you nudge it, it rolls back to the bottom.
• Low Center of Gravity: Objects in stable equilibrium usually have a low center of gravity. This means their weight is distributed in such a way that they naturally want to return to their original position, just like a pendulum swinging back to the middle.
• Potential Energy: In stable equilibrium, if you move the object, you’re lifting it against gravity, which increases its potential energy. When you let go, gravity pulls it back down to where it has the least potential energy, which is its stable position.

Examples:

• A Ball in a Bowl: If you place a ball inside a bowl and push it slightly, it will roll back to the center of the bowl.
• A Book on a Table: If you tilt a book on a table and then let go, it will fall back to its flat position.

So, stable equilibrium is all about balance and the natural tendency of objects to return to a position where they are stable and balanced.

Unstable Equilibrium

If displaced, the body moves further away from its original position. Picture a pencil standing on its point. It’s balanced just right, but if you tap it even slightly, it will fall over. This is an example of an unstable equilibrium.

In physics, an object is in unstable equilibrium if, after a slight nudge, it moves away from its original position and doesn’t come back. Here’s why:

• Repelling Force: When you push an object in unstable equilibrium, instead of a force pushing it back to where it started, the force pushes it further away. It’s like pushing a ball on top of a hill; it rolls down instead of going back up.
• High Center of Gravity: Objects in unstable equilibrium often have a high center of gravity. This means they’re more likely to topple over when disturbed because their weight is distributed in a way that doesn’t favor returning to the starting position.
• Potential Energy: In unstable equilibrium, moving the object slightly lowers its potential energy, which means gravity will pull it further in that direction, away from where it started.

Examples:

• Pencil on a Point: A pencil balanced on its point is in unstable equilibrium. Any disturbance will cause it to fall.
• Ball on a Hill: A ball placed at the very top of a hill is another example. If you push it, it will roll down the hill instead of staying put.

Unstable equilibrium is like being on the edge—any small push can lead to a big change. It’s a delicate balance that’s easily disrupted, and once it’s lost, the object won’t return to its initial position.

Neutral Equilibrium

If displaced, the body remains in its new position. Imagine you have a ball on a flat table. You give it a gentle push, and it stops wherever you leave it. It doesn’t roll back to its original spot, nor does it keep rolling away. This is what we call neutral equilibrium.

In physics, an object is in neutral equilibrium if, after a slight nudge, it stays in its new position. It doesn’t try to return to its original position (like in stable equilibrium), nor does it move further away (like in unstable equilibrium). Here’s why:

• No Restoring Force: When you push an object in neutral equilibrium, there’s no force pulling it back or pushing it further. It’s content to stay right where you left it.
• Flat Potential Energy Surface: The potential energy doesn’t change when you move the object. It’s like rolling a ball on a flat surface; the ball doesn’t care where it stops because every spot is as good as any other.
• Independence from Displacement: The object’s equilibrium doesn’t depend on where it is. Whether it’s here, there, or anywhere on the flat surface, it’s all the same in terms of energy and forces.

Examples:

• A Ball on a Flat Surface: Just like our example, a ball on a flat table will stay where you push it.
• A Hockey Puck on Ice: A hockey puck sliding on ice will keep moving in a straight line and stop without returning or moving away from its stopping point.

Also Read: Rigid Body

Principle of Moments

This principle states that for a body to be in equilibrium, the sum of the clockwise moments about any point must equal the sum of the counterclockwise moments about that same point.

Imagine you’re on a seesaw with a friend. You’re both trying to balance it so that neither of you is touching the ground. To do this, you both adjust your positions until the seesaw is level. This balancing act is a practical example of the Principle of Moments.

The Principle of Moments, also known as Varignon’s Theorem, is a fundamental concept in physics that helps us understand how different forces can balance each other out. It states that for an object to be in equilibrium (perfectly balanced), the total sum of the clockwise moments about any point (like the pivot of the seesaw) must be equal to the total sum of the anticlockwise moments about that same point.

• Moment: A moment is the turning effect of a force. It’s calculated by multiplying the force applied by the distance from the pivot point (where the seesaw turns).
• Clockwise and Anticlockwise Moments: If you push down on one end of the seesaw, you create a clockwise moment. If your friend pushes down on the other end, they create an anticlockwise moment.
• Balancing Moments: For the seesaw to be balanced, the clockwise and anticlockwise moments must be equal. This means the product of the force and the distance from the pivot must be the same for both sides.

The mathematical way to express this is:

\(\displaystyle \text{Total Clockwise Moments} = \text{Total Anticlockwise Moments} \)

Or, if we have two forces, (F₁) and (F₂), at distances (d₁) and (d₂) from the pivot, the equation would be:

\(\displaystyle F_1 \times d_1 = F_2 \times d_2 \)

This principle isn’t just for seesaws. It’s used in designing bridges, buildings, and even in understanding how our muscles work to move our bones. Engineers use it to make sure structures are stable and won’t topple over.

Solved Examples

Example 1: A uniform horizontal beam of length 4 meters and weight 200 N is supported at its ends by two ropes. If a weight of 300 N is suspended from the middle of the beam, calculate the tension in each rope.

Solution: Let’s denote the tensions in the ropes as (T₁) and ( T₂). Since the beam is in equilibrium, the sum of the vertical forces and the sum of the moments about any point must be zero. Resolving vertical forces:

\(\displaystyle T_1 + T_2 – 300 \, \text{N} – 200 \, \text{N} = 0 \)
\(\displaystyle T_1 + T_2 = 500 \, \text{N} \hspace{1cm}\) (1)

Taking moments about one end (where (T₂) acts):

\(\displaystyle T_1 \times 4 \, \text{m} – 300 \, \text{N} \times 2 \, \text{m} – 200 \, \text{N} \times 4 \, \text{m} = 0 \)
\(\displaystyle 4T_1 – 600 \, \text{Nm} – 800 \, \text{Nm} = 0 \)
\(\displaystyle 4T_1 = 1400 \, \text{Nm} \)
\(\displaystyle T_1 = 350 \, \text{N} \)

Substituting (T₁) into equation (1):

\(\displaystyle 350 \, \text{N} + T_2 = 500 \, \text{N} \)
\(\displaystyle T_2 = 150 \, \text{N} \)

Therefore, the tension in rope 1 (T₁) is ( 350 N) and the tension in rope 2 (T₂) is (150 N).

Example 2: A lamppost of weight 500 N stands on a horizontal surface. If the tension in the guy wire is 600 N and makes an angle of 30 degrees with the vertical, calculate the normal reaction force exerted by the ground.

Solution: Let (N) be the normal reaction force exerted by the ground. Since the lamppost is in equilibrium, the vertical component of the tension in the guy wire balances the weight of the lamppost. Resolving vertical forces:

\(\displaystyle N – 600 \, \text{N} \times \cos(30^\circ) – 500 \, \text{N} = 0 \)
\(\displaystyle N – 600 \times \frac{\sqrt{3}}{2} – 500 = 0 \)
\(\displaystyle N – 300\sqrt{3} – 500 = 0 \)
\(\displaystyle N = 500 + 300\sqrt{3} \)

Therefore, the normal reaction force exerted by the ground is \(\displaystyle 500 + 300\sqrt{3} \) N.

Example 3: A uniform sign of weight 400 N is hung by two ropes making angles of 30 degrees and 60 degrees with the horizontal. Calculate the tension in each rope.

Solution: Let (T₁) and (T₂) be the tensions in the ropes. Since the sign is in equilibrium, the vertical and horizontal components of the tension forces balance the weight of the sign. Resolving vertical forces:

\(\displaystyle T_1 \times \cos(60^\circ) + T_2 \times \cos(30^\circ) – 400 \, \text{N} = 0 \)
\(\displaystyle \frac{T_1}{2} + \frac{\sqrt{3}}{2}T_2 – 400 = 0 \hspace{1cm}\) (1)

Resolving horizontal forces:

\(\displaystyle T_1 \times \sin(60^\circ) – T_2 \times \sin(30^\circ) = 0 \)
\(\displaystyle \frac{\sqrt{3}}{2}T_1 – \frac{T_2}{2} = 0 \)
\(\displaystyle \sqrt{3}T_1 – T_2 = 0 \)
\(\displaystyle T_2 = \sqrt{3}T_1 \hspace{1cm}\) (2)

Substituting (T₂) from equation (2) into equation (1):

\(\displaystyle \frac{T_1}{2} + \frac{\sqrt{3}}{2}(\sqrt{3}T_1) – 400 = 0 \)
\(\displaystyle \frac{T_1}{2} + 3T_1 – 400 = 0 \)
\(\displaystyle \frac{7T_1}{2} = 400 \)
\(\displaystyle T_1 = \frac{800}{7} \, \text{N} \)

Substituting (T₁) into equation (2):

\(\displaystyle T_2 = \sqrt{3} \times \frac{800}{7} \, \text{N} \)
\(\displaystyle T_2 = \frac{800\sqrt{3}}{7} \, \text{N} \)

Therefore, the tension in rope 1 (T₁) is \(\displaystyle\frac{800}{7} \) N and the tension in rope 2 (T₂) is \(\displaystyle \frac{800\sqrt{3}}{7} \) N.

Example 4: A uniform rod of length 6 meters and weight 300 N is supported horizontally by two strings attached to its ends. If a weight of 400 N is hung at a distance of 3 meters from one end, calculate the tensions in the strings.

Solution: Let (T₁) and (T₂) be the tensions in the strings. Since the rod is in equilibrium, the sum of the vertical forces and the sum of the moments about any point must be zero. Resolving vertical forces:

\(\displaystyle T_1 + T_2 – 400 \, \text{N} – 300 \, \text{N} = 0 \)
\(\displaystyle T_1 + T_2 = 700 \, \text{N} \hspace{1cm}\) (1)

Taking moments about one end (where (T₂) acts):

\(\displaystyle T_1 \times 6 \, \text{m} – 400 \, \text{N} \times 3 \, \text{m} – 300 \, \text{N} \times 6 \, \text{m} = 0 \)
\(\displaystyle 6T_1 – 1200 \, \text{Nm} – 1800 \, \text{Nm} = 0 \)
\(\displaystyle 6T_1 = 3000 \, \text{Nm} \)
\(\displaystyle T_1 = 500 \, \text{N} \)

Substituting (T₁) into equation (1):

\(\displaystyle 500 \, \text{N} + T_2 = 700 \, \text{N} \)
\(\displaystyle T_2 = 200 \, \text{N} \)

Therefore, the tension in string 1 (T₁) is ( 500 N) and the tension in string 2 (T₂) is (200 N).

Example 5: A block of weight 500 N rests on an inclined plane making an angle of 30 degrees with the horizontal. If the coefficient of static friction between the block and the inclined plane is 0.3, calculate the minimum force required to keep the block in equilibrium.

Solution: To keep the block in equilibrium, the force applied parallel to the inclined plane (F) must balance the gravitational force acting down the plane and the force of static friction. Resolving forces parallel to the inclined plane:

\(\displaystyle F – f_s – W \sin(\theta) = 0 \)
\(\displaystyle F – \mu_s N – W \sin(\theta) = 0 \)
\(\displaystyle F – 0.3 \times N – 500 \times \sin(30^\circ) = 0 \)
\(\displaystyle F – 0.3N – 250 = 0 \hspace{1cm}\) (1)

Resolving forces perpendicular to the inclined plane:

\(\displaystyle N – W \cos(\theta) = 0 \)
\(\displaystyle N – 500 \times \cos(30^\circ) = 0 \)
\(\displaystyle N – 500 \times \frac{\sqrt{3}}{2} = 0 \)
\(\displaystyle N – 250\sqrt{3} = 0 \)
\(\displaystyle N = 250\sqrt{3} \hspace{1cm}\) (2)

Substituting (N) from equation (2) into equation (1):

\(\displaystyle F – 0.3 \times 250\sqrt{3} – 250 = 0 \)
\(\displaystyle F – 75\sqrt{3} – 250 = 0 \)
\(\displaystyle F = 75\sqrt{3} + 250 \)

Therefore, the minimum force required to keep the block in equilibrium is \(\displaystyle 75\sqrt{3} + 250 \) N.

FAQs