Heat, Internal Energy, and Work

The concept of heat as a form of energy that flows from a hotter body to a cooler one was developed over time. In the 18th century, scientists like Joseph Black and James Watt studied heat in the context of steam engines, leading to the formulation of the concept of latent heat and the improvement of steam engines.

The idea of internal energy is rooted in the kinetic theory of gases, which was developed in the 19th century. Scientists like Rudolf Clausius and James Clerk Maxwell contributed to this theory by describing how the motion of molecules constitutes the internal energy of a system.

The concept of work in physics was formalized by French mathematician Gaspard-Gustave de Coriolis in 1829. It was further developed in the context of thermodynamics, particularly through the work of James Prescott Joule in the mid-19th century, who demonstrated the equivalence of mechanical work and heat.

These historical developments led to the formulation of the First Law of Thermodynamics, which states that energy cannot be created or destroyed, only transformed from one form to another. This law ties together the concepts of heat, internal energy, and work, showing that they are different manifestations of the same fundamental entity: energy.

Internal Energy

Internal Energy, often denoted as (U), is essentially the energy stored within a system. It’s the sum of all the kinetic and potential energies of the particles (like atoms and molecules) that make up the system.

Imagine a sealed container filled with gas. The gas molecules are constantly moving in random directions and colliding with each other and the walls of the container. This movement is a form of kinetic energy. Additionally, there might be forces between the molecules, like attraction or repulsion, which contribute to potential energy.

The total kinetic energy relates to the temperature of the gas: the higher the temperature, the faster the molecules move, and thus, the greater their kinetic energy. The potential energy depends on the interactions between the molecules, which can change if the gas is compressed or expanded.

Internal Energy Formula

The internal energy of a system can change if heat is added or removed, or if work is done on or by the system. The formula that represents this is:

\(\displaystyle \Delta U = Q – W \)

Here, (∆U) is the change in internal energy, (Q) is the heat added to the system, and (W) is the work done by the system.

Relation between Enthalpy and Internal Energy

Enthalpy (H) is another important concept and is related to internal energy. It’s the measure of the total energy of a system, including the energy needed to create space for the system by pushing against the surrounding atmosphere. The relationship is given by:

\(\displaystyle H = U + PV \)

Internal energy is like the “energy account” of a system, reflecting the balance of energy going in and out due to heat and work.

Factors that affect the amount of heat flow

• Temperature Difference: The greater the difference, the more heat flows.
• Material: Some materials conduct heat better than others.
• Surface Area: Larger areas transfer more heat.
• Duration: The longer the contact, the more heat is transferred.

Also Read: First Law of Thermodynamics

Heat

Heat is a form of energy that is transferred between two objects or systems due to a temperature difference. It’s important to note that heat is not the same as temperature; rather, it is the energy in transit.

What is Heat?

Imagine you’re holding a cup of hot coffee. The warmth you feel is heat transferring from the coffee to your hand. This transfer happens because the coffee is at a higher temperature than your hand. The molecules in the hot coffee are moving faster and have more kinetic energy compared to the molecules in your hand. When they come into contact, energy is transferred from the faster-moving molecules (hot coffee) to the slower-moving molecules (your hand), which you perceive as heat.

How Does Heat Transfer?

• Conduction: Direct contact transfer, like a metal spoon getting hot in a pot of soup.
• Convection: Transfer through fluids (liquids or gases), like warm air rising and cool air descending.
• Radiation: Transfer through electromagnetic waves, like the sun warming your face.

Factors Affecting Heat Transfer

• Temperature Difference: The greater the difference, the faster the heat transfer.
• Material Properties: Some materials conduct heat better than others. Metals, for example, are good conductors of heat.
• Surface Area and Thickness: A larger area or thinner material can transfer heat more quickly.
• Density and Specific Heat: Materials with lower density or higher specific heat can absorb more heat without a significant temperature change.

Heat is measured in units of energy, such as joules (J) in the International System of Units (SI). Another common unit is the calorie, which is the amount of heat required to raise the temperature of one gram of water by one degree Celsius.

Heat and Work

In thermodynamics, heat and work are related concepts. While heat is energy transferred due to temperature difference, work is energy transferred when a force moves an object over a distance. Both can change the internal energy of a system. Heat and Work are both ways that energy can be transferred into or out of a system. They are related but are not the same thing. The relationship between them is best described by the First Law of Thermodynamics, which states:

\(\displaystyle \Delta U = Q – W \)

• If you add heat (Q) to a system, its internal energy (U) increases, unless the system does work (W) on its surroundings, which would use up some of that energy.
• Conversely, if a system does work on its surroundings, it might need to use up some of its internal energy, making it cooler unless heat is added to make up for it.

In a steam engine, heat is added to water to create steam, which then does work by moving pistons. The heat energy (from burning coal, for example) is converted into mechanical work.

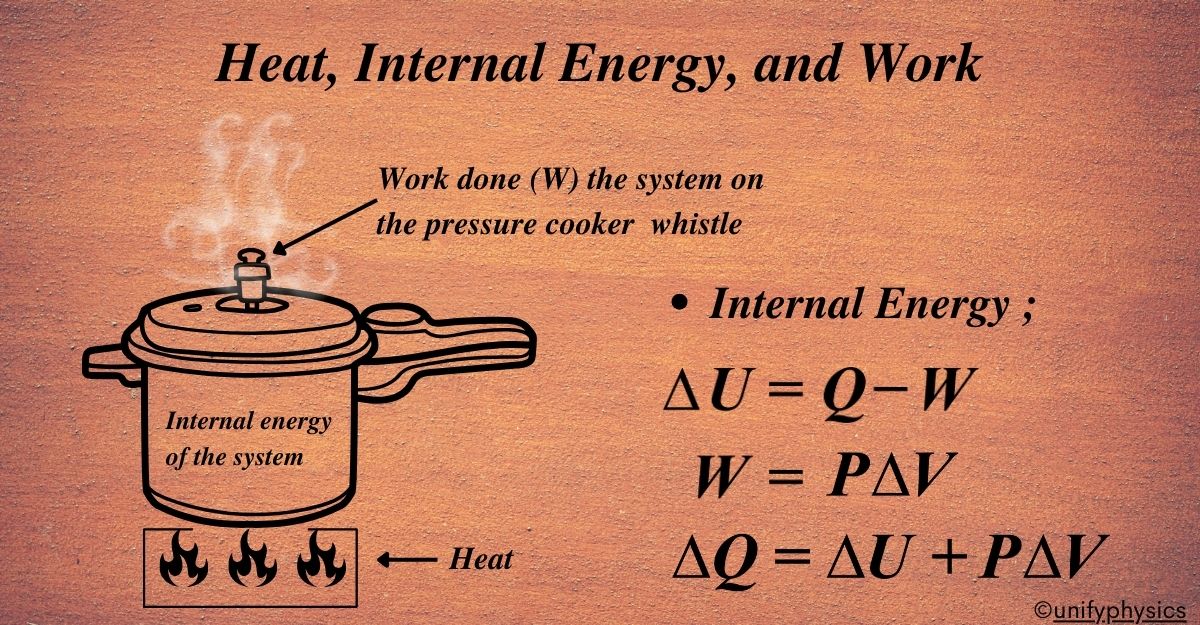
A pressure cooker is a simple example to illustrate the concepts of heat, internal energy, and work in thermodynamics.

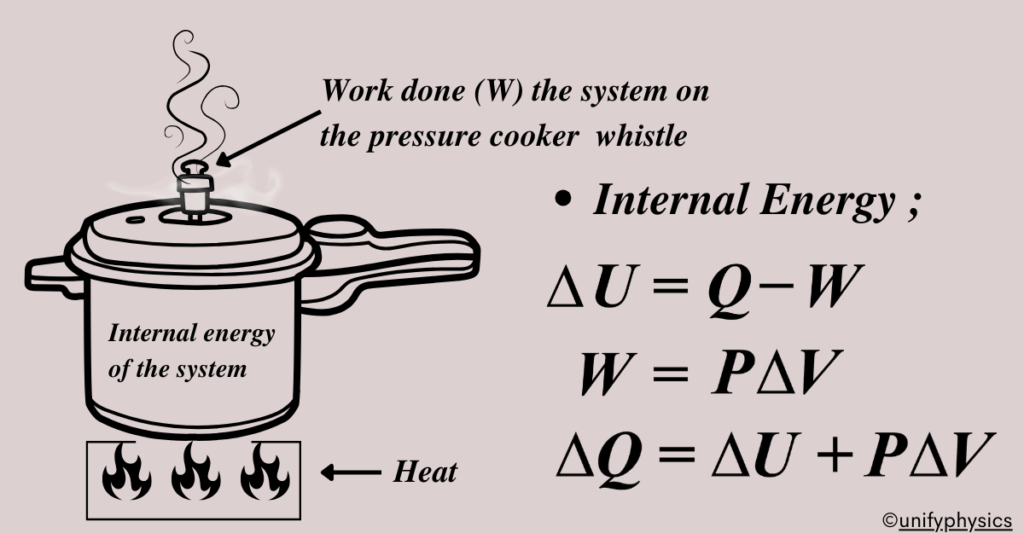
In a pressure cooker, heat is the energy that is transferred from the stove to the cooker. It flows because of the temperature difference between the burner and the cooker. The heat energy causes the water inside the cooker to increase in temperature and eventually boil, turning into steam.

The internal energy of the system, which in this case includes the water and the steam inside the cooker, is the sum of the kinetic and potential energies of its molecules. As heat is added, the internal energy increases, leading to a rise in temperature and pressure inside the cooker. The molecules move faster (increased kinetic energy) and the distance between them increases (increased potential energy).

Work in this context is done when the steam pushes up against the lid of the cooker, creating a force over a distance. In an ideal scenario where the lid is fixed and doesn’t move, no work is done since there is no displacement. However, in reality, the steam might push the safety valve or whistle, doing work on the surroundings.

Thermodynamic Cycle of a Pressure Cooker

• Heat is added to the cooker from the stove, increasing the internal energy of the water and converting it to steam.
• As steam forms, it increases the pressure inside the cooker. The internal energy of the steam is higher than that of water at the same temperature.
• The cooker reaches a steady state where the pressure is high enough to raise the boiling point of water, cooking the food faster.
• Once removed from the stove, the cooker begins to cool. The steam condenses back into water, releasing heat and decreasing the internal energy.

Work

Work is done when a force is applied to an object, and it moves. In thermodynamics, work can be done by the system (like expanding gas pushing a piston) or on the system (like compressing a gas)

Imagine you have a syringe filled with air, and you’re pressing down on the plunger. You’re doing work on the air inside because you’re applying a force over a distance. In thermodynamics, this is exactly how work is defined: it’s the energy transferred when a force causes a displacement. The work done by or on a system can be calculated using the formula:

\(\displaystyle W = P \Delta V \)

• Expansion Work: When a gas expands, it does work on its surroundings. If you release the plunger of the syringe, the air pushes it back out—that’s expansion work.
• Compression Work: Conversely, when you press the plunger, you’re doing compression work on the gas.

In thermodynamics, work is one of the two main ways energy is transferred into or out of a system—the other being heat. When a system does work, it uses its internal energy to exert a force over a distance. In engines and refrigerators, which operate on thermodynamic cycles, work is an essential part of the process. For example, in a car engine, the combustion of fuel does work on the pistons, which then turn the wheels.

The concept of work in thermodynamics is closely tied to the First Law of Thermodynamics, which is essentially the law of conservation of energy applied to thermal systems. It tells us that the energy of the universe is constant, and energy can only be transferred, not created or destroyed.

Solved Examples

Problem 1: One mole of an ideal gas expands isothermally at a temperature of 300 K from a volume of 10 L to 20 L. Calculate the work done by the gas during the expansion.

Solution: For an isothermal process, the work done by an ideal gas is given by:

\(\displaystyle W = nRT \ln\left(\frac{V_f}{V_i}\right) \)

Given:

• (n = 1) mole
• (R = 8.314 J/mol·K)
• (T = 300 K)
• (\(\displaystyle V_i = 10 \, \text{L} = 10 \times 10^{-3} \, \text{m}^3\))
• (\(\displaystyle V_f = 20 \, \text{L} = 20 \times 10^{-3} \, \text{m}^3\) )

Substituting the values:

\(\displaystyle W = 1 \times 8.314 \times 300 \ln\left(\frac{20 \times 10^{-3}}{10 \times 10^{-3}}\right) \)
\(\displaystyle W = 2494.2 \ln(2) \)
\(\displaystyle W = 2494.2 \times 0.693 \)
W = 1728.4 J

The work done by the gas during the isothermal expansion is 1728.4 J.

Problem 2: An ideal gas undergoes an adiabatic process where its initial temperature is 400 K, and the final temperature is 300 K. If the number of moles of the gas is 2 and the molar specific heat capacity at constant volume (C_V) is 20 J/mol·K, calculate the change in internal energy.

Solution: For an adiabatic process, the change in internal energy (∆U) is given by:

\(\displaystyle \Delta U = n C_V \Delta T \)

Given:

• (n = 2) moles
• (C_V = 20 J/mol·K)
• (\(\displaystyle \Delta T = T_f – T_i = 300 \, \text{K} – 400 \, \text{K} = -100 \, \text{K} \))

Substituting the values:

\(\displaystyle\Delta U = 2 \times 20 \times (-100) \)
\(\displaystyle \Delta U = -4000 \, \text{J} \)

The change in internal energy is -4000 J.

Problem 3: A gas undergoes an isobaric expansion at a pressure of 2 atm from a volume of 5 L to 10 L. The initial temperature of the gas is 300 K. Calculate the heat transferred to the gas if the molar specific heat at constant pressure (C_P) is 29 J/mol·K and the number of moles is 1.

Solution: For an isobaric process, the heat transferred (Q) is given by:

\(\displaystyle Q = n C_P \Delta T \)

First, we need to find (∆T) using the ideal gas law:

\(\displaystyle P V_i = n R T_i \)
\(\displaystyle P V_f = n R T_f \)

Given:

• (\(\displaystyle P = 2 \, \text{atm} = 2 \times 1.013 \times 10^5 \, \text{Pa}\)
• (\(\displaystyle V_i = 5 \, \text{L} = 5 \times 10^{-3} \, \text{m}^3\)
• (\(\displaystyle V_f = 10 \, \text{L} = 10 \times 10^{-3} \, \text{m}^3\)
• (T_i = 300 K)
• (R = 8.314 J/mol·K)

Using (P V_i = n RT_i):

\(\displaystyle 2 \times 1.013 \times 10^5 \times 5 \times 10^{-3} = 1 \times 8.314 \times 300 \)
\(\displaystyle 1013 \times 5 = 8.314 \times 300 \)
\(\displaystyle T_f = \frac{P V_f}{n R} = \frac{2 \times 1.013 \times 10^5 \times 10 \times 10^{-3}}{8.314} \)

\(\displaystyle T_f = \frac{2 \times 1013 \times 10}{8.314} \)
\(\displaystyle T_f = \frac{20260}{8.314} \)
\(\displaystyle T_f = 2437.74 \, \text{K} \)

So, (\(\displaystyle\Delta T = T_f – T_i = 2437.74 – 300 = 2137.74 \, \text{K}\) )

Substituting the values:

\(\displaystyle Q = 1 \times 29 \times 2137.74 \)
\(\displaystyle Q = 62094.46 \, \text{J} \)

The heat transferred to the gas is 62094.46 J.

Problem 4: Calculate the work done by an ideal gas during an isobaric expansion from a volume of 2 L to 5 L at a constant pressure of 3 atm.

Solution: For an isobaric process, the work done by the gas (W) is given by:

\(\displaystyle W = P \Delta V \)

Given:

• (\(\displaystyle P = 3 \, \text{atm} = 3 \times 1.013 \times 10^5 \, \text{Pa} \))
• (\(\displaystyle V_i = 2 \, \text{L} = 2 \times 10^{-3} \, \text{m}^3\))
• (\(\displaystyle V_f = 5 \, \text{L} = 5 \times 10^{-3} \, \text{m}^3\) )

Substituting the values:

\(\displaystyle W = 3 \times 1.013 \times 10^5 \times (5 \times 10^{-3} – 2 \times 10^{-3}) \)
\(\displaystyle W = 3 \times 1.013 \times 10^5 \times 3 \times 10^{-3} \)
\(\displaystyle W = 3 \times 1.013 \times 300 \)
W = 91170 J

The work done by the gas is 91170 J.

Problem 5: An ideal gas is heated at constant volume from 300 K to 600 K. If the number of moles is 2 and the molar specific heat capacity at constant volume (C_V) is 12.5 J/mol·K, calculate the change in internal energy.

Solution: For an isochoric process, the change in internal energy (∆U) is given by:

\(\displaystyle \Delta U = n C_V \Delta T \)

Given:

• (n = 2) moles
• (\(\displaystyle C_V = 12.5 \, \text{J/mol·K} \))
• (\(\displaystyle\Delta T = T_f – T_i = 600 \, \text{K} – 300 \, \text{K} = 300 \, \text{K} \))

Substituting the values:

\(\displaystyle \Delta U = 2 \times 12.5 \times 300 \)
\(\displaystyle \Delta U = 7500 \, \text{J} \)

The change in internal energy is 7500 J.

Problem 6: One mole of an ideal gas is heated from 300 K to 400 K at constant pressure. Given the molar specific heat capacity at constant pressure (C_P) is 20 J/mol·K, calculate the heat supplied to the gas.

Solution: For an isobaric process, the heat supplied (Q) is given by:

\(\displaystyle Q = n C_P \Delta T \)

Given:

• (n = 1) mole
• (C_P = 20 J/mol·K)
• (\(\displaystyle \Delta T = T_f – T_i = 400 \, \text{K} – 300 \, \text{K} = 100 \, \text{K} \))

Substituting the values:

\(\displaystyle Q = 1 \times 20 \times 100 \)
Q = 2000 J

The heat supplied to the gas is 2000 J.

FAQs