Kepler’s Law of Planetary Motion

The story of Kepler’s Laws begins with the meticulous observations of the heavens by Tycho Brahe, a Danish nobleman and astronomer. Brahe’s detailed records of planetary positions were unmatched at the time and provided the foundation for a breakthrough in our understanding of the solar system.

Johannes Kepler, a German mathematician and astronomer, became Brahe’s assistant. After Brahe’s death, Kepler inherited his extensive observations. Kepler was a brilliant thinker who sought to understand the order behind the apparent chaos in the heavens. He believed that the universe was constructed according to geometric principles and that the motions of celestial bodies followed mathematical laws.

Kepler set out to find these laws, and after years of painstaking analysis, he succeeded. He published his first two laws in 1609 and the third law in 1618. These laws were revolutionary because they challenged the prevailing belief in perfectly circular orbits, which had been the dominant view since the time of Aristotle and Ptolemy and had been slightly modified by Copernicus.

Kepler’s Laws described the orbits of planets as ellipses rather than circles, with the Sun at one focus of the ellipse, not at the center. This was a radical departure from the circular orbits that had been assumed for centuries. Kepler’s work laid the groundwork for Isaac Newton’s laws of motion and universal gravitation, which would come later in the 17th century.

Kepler’s Laws were empirical, meaning they were based on observation rather than derived from first principles. It wasn’t until Newton formulated his theory of gravitation that the reason behind Kepler’s Laws became clear: they were a natural consequence of a force that decreased with the square of the distance between two bodies.

Motion of Particles

Bounded Motion

This refers to motion that is restricted within a certain area. In the solar system, planets exhibit bounded motion as they are confined to their orbits around the Sun.

In the world of physics, when we talk about the motion of particles, we often categorize it based on whether the motion is restricted or not. Bounded motion is a type of motion where a particle is restricted within certain limits—it’s like being on a leash that you can’t see but feel.

Imagine you’re playing with a yo-yo. You can swing it around, and it goes up and down, but no matter what, it can’t escape the length of its string. This is similar to how bounded motion works for particles. They can move, but only within the confines of an invisible boundary set by forces acting upon them.

These forces create what we call a potential well—a valley in the landscape of potential energy. The particle can move within this valley, but it doesn’t have enough energy to climb out of it. It’s trapped, but within this trap, it has the freedom to move around.

In bounded motion, the total energy of the particle is always less than the potential energy at the boundary. This means the particle has a negative total energy. When the particle reaches the edge of its allowed region, its kinetic energy drops to zero, and all its energy is potential.

Examples:

• Planets and Moons: Just like the yo-yo, planets and moons are in bounded motion around their stars and planets, respectively. They are held in their orbits by the gravitational pull of the larger body they orbit.
• Electrons in Atoms: Electrons bound to an atom move in defined regions around the nucleus. They have specific energy levels and can’t just wander off without an input of additional energy.

Bounded motion is a beautiful example of how even in the vast openness of space, everything is tethered by invisible forces, creating a harmonious balance in the universe. It’s a concept that not only explains the motion of particles but also inspires awe in the orderliness of nature.

Unbounded Motion

Unbounded motion is not restricted to a specific area. Comets that come from the outer reaches of the solar system and then leave are examples of unbounded motion. When we talk about Unbounded Motion in physics, we’re discussing a scenario where particles are not held back by any potential barriers—they have the freedom to move without limits.

Unbounded motion occurs when a particle has enough kinetic energy to overcome any potential energy barriers. It’s like a spacecraft that has enough fuel to break free from Earth’s gravity and travel into deep space. In this state, the particle is not bound to any particular region and can move infinitely far away.

For unbounded motion to occur, the kinetic energy of the particle must be greater than or equal to the potential energy at any point. This means the total mechanical energy of the particle is positive or zero. When this happens, there are no ‘valleys’ or ‘wells’ in the potential energy landscape that can contain the particle’s motion.

Examples:

• Space Probes: Just like the Voyager spacecraft, which have left the solar system, particles in unbounded motion are not confined to a specific area and can travel great distances.
• Alpha Particles: In the famous Rutherford scattering experiment, alpha particles are scattered by the nucleus of an atom. Some of these particles have enough energy to escape the attractive force of the nucleus and move away indefinitely.

In celestial mechanics, unbounded trajectories can be described by conic sections—specifically, parabolas and hyperbolas. These shapes represent the paths that objects like comets or asteroids might take as they pass by a planet or the Sun and then continue on their way, not bound to return.

How does unbounded motion relate to escape velocity?

Unbounded motion and escape velocity are closely related concepts in physics, especially in the context of celestial mechanics. Unbounded motion is the result of achieving or exceeding the escape velocity, allowing an object to leave the gravitational influence of a celestial body and move into space freely, without being pulled back.

Escape velocity is the minimum speed needed for an object to break free from the gravitational pull of a celestial body without further propulsion. It’s like hitting the gas pedal just enough to get your car up and over a hill, but in space, this ‘hill’ is the gravitational well created by a planet or star.

Unbounded motion occurs when a particle or object has enough kinetic energy to overcome the gravitational potential energy of a larger body. If this kinetic energy is equal to or greater than the energy required to escape the gravitational pull, the object will have unbounded motion—it will not return and will continue moving away indefinitely.

The formula for escape velocity (V_e) can be derived from the concept of conservation of energy and is given by:

\(\displaystyle V_e = \sqrt{2gR} \)

where (g) is the acceleration due to gravity at the surface of the celestial body, and (R) is the radius of the body.

For an object in a circular orbit, the orbital velocity (V_o) is given by:

\(\displaystyle V_o = \sqrt{gR} \)

Escape velocity is ( \(\displaystyle\sqrt{2}\) ) times the orbital velocity:

\(\displaystyle V_e = \sqrt{2} V_o \)

This means that escape velocity is directly proportional to orbital velocity. If an object achieves a speed equal to the escape velocity, it will enter unbounded motion and will not be gravitationally bound to the celestial body anymore.

Kepler’s First Law (Law of Orbits)

Kepler’s First Law states that planets move in elliptical orbits with the Sun at one focus. This means that the distance between a planet and the Sun changes as the planet travels along its orbit.

Imagine you have a planet orbiting the Sun. Kepler’s First Law tells us that the path this planet takes around the Sun isn’t a perfect circle, as many people once thought. Instead, it’s like a slightly stretched or squished circle called an “ellipse.” Picture it like a flattened circle.

“All planets move in elliptical orbits with the Sun situated at one of the foci of the ellipse.”

An ellipse is a shape that looks like a flattened or stretched circle. The Sun isn’t at the center of this circle, but a bit to the side. The two ends of the ellipse are the closest point (perihelion) and the farthest point (aphelion) from the Sun.

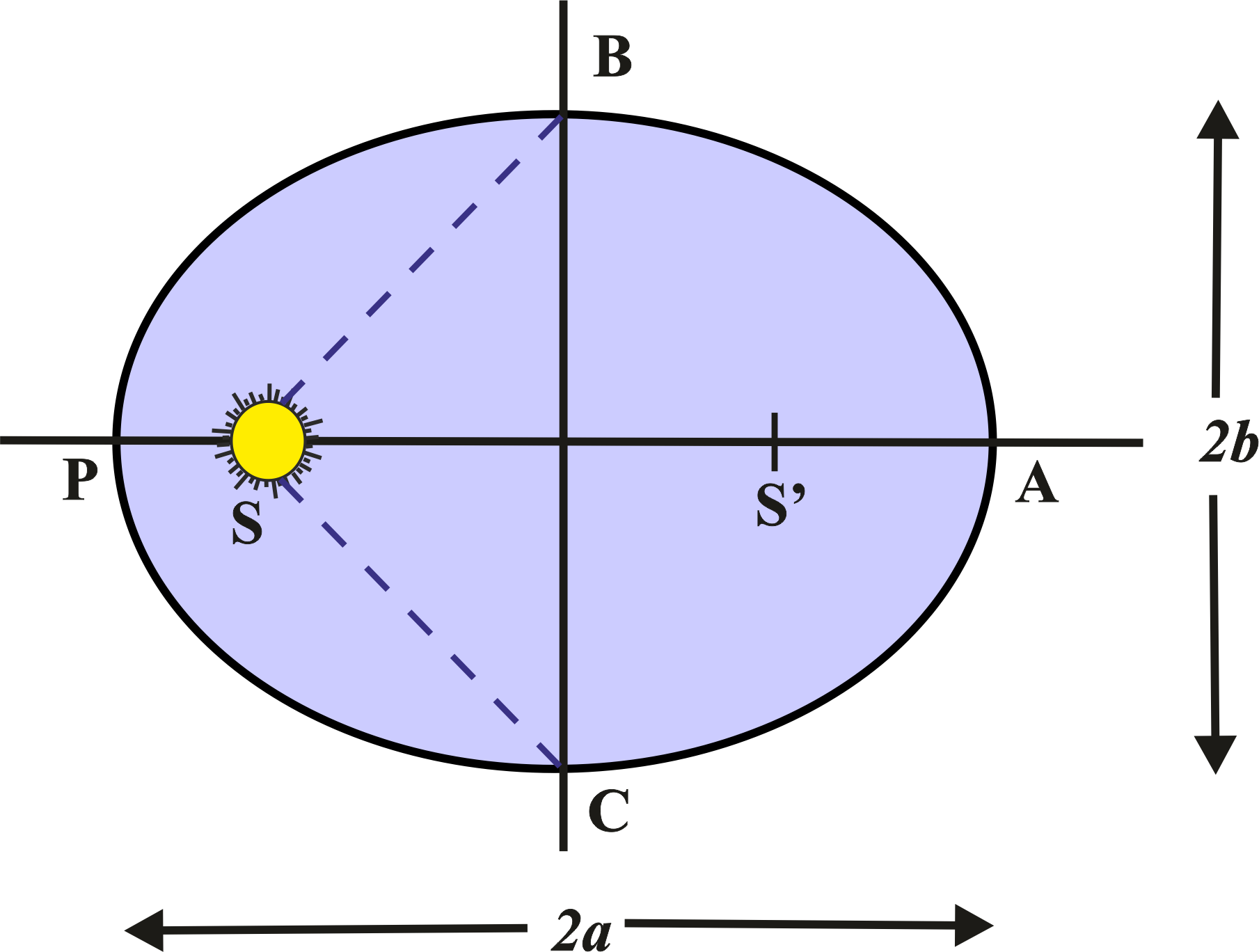
There are two special points inside the ellipse. If you think of the Sun as a spotlight, it’s at one of these points, called a “focus.” The other focus is just an empty point in space. An ellipse is characterized by two axes – the longer semi-major axis (a) and the shorter semi-minor axis (b). The Sun is situated at one of the foci, and as a planet travels along its elliptical orbit, it experiences varying distances from the Sun.

For the specific case of a planet orbiting the Sun, the Sun is located at one of the foci, and the position of the planet can be described by the polar equation:

\(\displaystyle r(\theta )=\frac{{a(1-{{e}^{2}})}}{{1+e\cos (\theta )}}\)

where r is the distance between the Sun and the planet, θ is the angle between the line connecting the Sun and the planet and a reference line, a is the semi-major axis, and e is the eccentricity of the ellipse. The eccentricity (e) of an ellipse measures how much it is stretched out. It ranges from 0 (for a perfect circle) to values closer to 1 (for a more elongated ellipse). The greater the eccentricity, the more elongated the orbit.

The eccentricity (e) of the ellipse measures how elongated or flattened the orbit is. For a circle, the eccentricity is zero, indicating a perfect circle. As the eccentricity increases, the ellipse becomes more elongated. Kepler’s First Law gave us a more accurate understanding of how planets move, and it set the stage for further discoveries about the laws of motion and gravity.

How does Kepler’s First Law relate to the concept of gravity?

Kepler’s First Law is deeply intertwined with the concept of gravity. While Kepler himself did not know the underlying cause of the planetary motions he described, his First Law laid the groundwork for Isaac Newton’s theory of universal gravitation.

Gravity is the force that attracts two bodies towards each other. In the context of the solar system, it’s the force that pulls planets towards the Sun. However, planets don’t fall into the Sun because they also have a tangential velocity that keeps them moving in an orbit.

For a planet to revolve in a fixed orbit, the gravitational force between the Sun and the planet must balance the centrifugal force due to the planet’s motion. This balance of forces keeps the planets in their elliptical orbits as described by Kepler’s First Law.

Newton showed that the motion of bodies subject to a central gravitational force need not always follow the elliptical orbits specified by Kepler but can take paths defined by other conic sections, depending on the total energy of the body. For planets in our solar system, this central force is gravity, which results in the elliptical orbits Kepler observed.

The gravitational force (F_g) that governs the orbits is given by Newton’s law of universal gravitation:

\(\displaystyle F_g = G \frac{m_1 m_2}{r^2} \)

where (G) is the gravitational constant, (m₁) and (m₂) are the masses of the Sun and the planet, and (r) is the distance between their centers.

For a planet in orbit, this gravitational force provides the necessary centripetal force (F_c) to keep it moving in its path:

\(\displaystyle F_c = \frac{m v^2}{r} \)

where (m) is the mass of the planet and (v) is its orbital velocity.

Kepler’s First Law states that planets move in elliptical orbits with the Sun at one focus. The shape of the orbit (ellipse) is maintained because the gravitational force acts as a centripetal force, pulling the planet towards the Sun and keeping it moving along that elliptical path.

Kepler’s First Law and the concept of gravity are fundamentally connected. Kepler’s observations of the elliptical orbits led to the understanding that there must be a force—gravity—causing these motions. Newton’s later work confirmed this, showing that gravity not only keeps the planets in their orbits but also explains why those orbits are elliptical.

Kepler’s Second Law – The Law of Equal Areas

Kepler’s Second Law, also known as the Law of Equal Areas, provides insight into the speed of a planet as it moves along its elliptical orbit around the Sun. When a planet orbits the Sun, it doesn’t move at a constant speed. Instead, it speeds up when it’s closer to the Sun and slows down when it’s farther away. However, if you connect the planet to the Sun with an imaginary line, the area it sweeps out in a certain amount of time is always the same.

” As a planet orbits the Sun, the line segment joining the planet and the Sun sweeps out equal areas in equal intervals of time.”

Kepler’s Second Law builds on the idea that a planet’s orbit is an ellipse (Kepler’s First Law). As a planet moves along its elliptical orbit, it experiences varying gravitational forces from the Sun. When the planet is closer (perihelion), the gravitational pull is stronger, causing it to move faster. Conversely, when it is farther away (aphelion), the gravitational pull weakens, and the planet slows down.

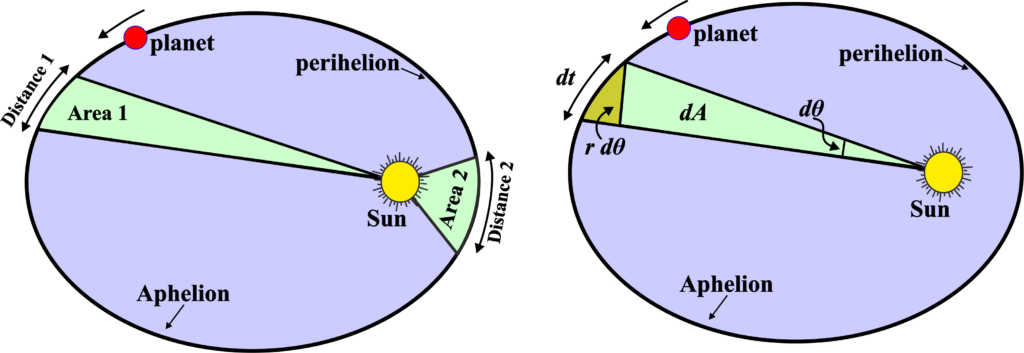
The mathematical expression for Kepler’s Second Law involves the conservation of angular momentum. In polar coordinates, the law can be stated as.

\(\displaystyle \frac{1}{2}{{r}^{2}}\frac{{d\theta }}{{dt}}=constant\)

Where r is the distance from the Sun (radius vector), θ is the angle between the line joining the planet and the Sun and a reference direction, and dt/dθ​ is the rate at which this angle changes with time.

dA/dt represents the rate of change of velocity with time. Hence, it is the areal velocity.

\(\displaystyle \frac{{{{r}^{2}}}}{2}\frac{{d\theta }}{{dt}}=constant\)

\(\displaystyle \frac{{dA}}{{dt}}=\frac{1}{2}.{{r}^{2}}.\frac{{d\theta }}{{dt}}\)

The angular momentum is given by,

\(\displaystyle L=m.{{r}^{2}}.\frac{{d\theta }}{{dt}}\)

\(\displaystyle \Rightarrow {{r}^{2}}.\frac{{d\theta }}{{dt}}=\frac{L}{m}\)

\(\displaystyle \frac{{dA}}{{dt}}=\frac{L}{{2m}}\)

The velocity at which a planet sweeps out an area in its orbit is equivalent to half of the angular momentum divided by the mass. In the planet-sun system, where the only force at play is the radial gravitational force, the conservation of angular momentum becomes crucial. The term L/2m remains constant, leading to the conclusion that the rate of change of the swept area with respect to time (dA/dt) is also a constant. Consequently, Kepler’s second law is a consequence of the conservation of angular momentum.

Despite these speed changes, the product of the radius vector and the speed (or rate of change of angle with time) remains constant. In practical terms, this means that when a planet sweeps out a larger area in a certain time period near aphelion, it compensates by moving slower, and when it sweeps out a smaller area near perihelion, it does so at a faster pace.

Kepler’s Third Law – The Law of Periods

Kepler’s Third Law, known as the Law of Periods, this law establishes a profound connection between the time it takes for a planet to complete its orbit (orbital period) and the dimensions of its elliptical path around the Sun.

The square of the orbital period (the time it takes for a planet to complete one orbit around the Sun) of a planet is directly proportional to the cube of the semi-major axis of its orbit.

Orbital period refers to the time it takes for a planet to complete one full orbit around the Sun, for example, Earth’s orbital period is one year. Mathematically, Kepler’s Third Law can be expressed as:

\(\displaystyle {{T}^{2}}=\frac{{4{{\pi }^{2}}}}{{GM}}{{a}^{3}}\)

\(\displaystyle {{T}^{2}}\propto {{a}^{3}}\)

Where T is the orbital period (time for one complete orbit), and a is the semi-major axis of the planet’s elliptical orbit.

This law implies that if you know the distance of a planet from the Sun, you can calculate how long it takes to orbit the Sun, and vice versa. For example, Earth is 1 astronomical unit (AU) away from the Sun and takes 1 year to orbit it. A planet that is 2 AU away from the Sun would take roughly 2.8 years to complete an orbit because (\(\displaystyle 2^3)^{1/2} = 2.8 \)).

Kepler referred to this law as the “harmonic law” because it shows a harmonious relationship between the distances of the planets from the Sun and their orbital periods. It’s like a cosmic symphony where each planet’s motion follows a precise pattern in relation to its position in the solar system.

Later, Isaac Newton showed that Kepler’s Third Law was a consequence of his laws of motion and the law of universal gravitation. This means that the same law applies to any two objects in space that are orbiting each other due to gravity.

Kepler’s Third Law is not just theoretical; it has practical uses in astronomy and space exploration. It helps scientists calculate the mass of celestial bodies and plan the trajectories of spacecraft. It’s also used to find exoplanets orbiting stars other than the Sun.

Derivation: The gravitational force between two masses (the Sun and a planet) is given by:

\(\displaystyle F = G \frac{Mm}{r^2} \)

where (r) is the distance between the two masses. For a planet in a circular orbit, the gravitational force provides the necessary centripetal force:

\(\displaystyle F_c = \frac{mv^2}{r} \)

Equating the gravitational force to the centripetal force:

\(\displaystyle G \frac{Mm}{r^2} = \frac{mv^2}{r} \)

The orbital velocity (v) of the planet is the distance traveled in one orbit (the circumference of the orbit, (\(\displaystyle 2\pi r \)) divided by the orbital period (T):

\(\displaystyle v = \frac{2\pi r}{T} \)

Substitute (v) into the centripetal force equation and solve for ( T² ):

\(\displaystyle G \frac{Mm}{r^2} = \frac{m(2\pi r/T)^2}{r} \)

Simplifying, we get:

\(\displaystyle T^2 = \frac{4\pi^2}{GM} \cdot r^3 \)

For elliptical orbits, (r) is replaced with the semi-major axis (a), giving us Kepler’s Third Law:

\(\displaystyle T^2 = \frac{4\pi^2}{GM} \cdot a^3 \)

This derivation shows that the orbital period of a planet depends only on its average distance from the Sun, not on the mass of the planet. It’s a powerful result that allows astronomers to calculate the distance of planets from their stars, both in our solar system and in exoplanetary systems.

Law of Conservation of Angular Momentum

To derive the expression that relates Kepler’s Law of Areas to the Law of Conservation of Momentum, we’ll walk through the physics concepts step by step. Kepler’s Second Law states that the line segment joining a planet to the Sun sweeps out equal areas during equal intervals of time. This means that a planet moves faster when it is closer to the Sun and slower when it is farther away.

The Law of Conservation of Angular Momentum states that if no external torque acts on a system, the angular momentum of the system remains constant.

The angular momentum of a planet with respect to the Sun is given by:

\(\displaystyle L = mvr \)

where (m) is the mass of the planet, (v) is its tangential velocity, and (r) is the distance from the Sun to the planet. As the planet orbits, it sweeps out an area. The area (A) swept out over a small time interval (dt) is:

\(\displaystyle dA = \frac{1}{2} r^2 d\theta \)

where (\(\displaystyle d\theta \)) is the small change in the angle as the planet moves.The rate at which the area is swept out is:

$$ \frac{dA}{dt} = \frac{1}{2} r^2 \frac{d\theta}{dt} $$

Since ( \(\displaystyle\frac{d\theta}{dt} \)) is the angular velocity (\(\displaystyle\omega\)), and (\(\displaystyle \omega = \frac{v}{r} \)), we can substitute to get:

\(\displaystyle \frac{dA}{dt} = \frac{1}{2} rv \)

Because angular momentum is conserved, (L) is constant, and so is (\(\displaystyle \frac{dA}{dt}\) ). Therefore, we can relate (L) to the area sweep rate:

\(\displaystyle L = mvr = 2m \frac{dA}{dt} \)

This shows that the rate at which the planet sweeps out area is directly related to its angular momentum. Since ( \(\displaystyle\frac{dA}{dt} \)) is constant, the planet sweeps out equal areas in equal times, which is Kepler’s Law of Areas.

The final expression relating the Law of Areas to the Conservation of Angular Momentum is:

\(\displaystyle \frac{dA}{dt} = \frac{L}{2m} \)

This equation tells us that the constant rate at which a planet sweeps out area (Kepler’s Second Law) is a manifestation of the conservation of angular momentum.

Newton’s Laws and Kepler’s Laws

The relationship between Newton’s Laws and Kepler’s Laws is like uncovering the hidden threads that connect the motion of celestial bodies to the fundamental principles of mechanics.

Isaac Newton’s laws describe the relationship between a body and the forces acting upon it, and its motion in response to those forces. They are:

• Law of Inertia: A body remains at rest or in uniform motion unless acted upon by a force.
• Law of Acceleration: The force on an object is equal to its mass times its acceleration (F = ma).
• Law of Action and Reaction: For every action, there is an equal and opposite reaction.

Johannes Kepler’s laws describe how planets move around the Sun:

• Law of Orbits: Planets move in elliptical orbits with the Sun at one focus.
• Law of Areas: A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
• Law of Periods: The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.

Newton’s and Kepler’s laws are intertwined through the force of gravity. Newton’s universal law of gravitation states that every point’s mass attracts every other point’s mass by a force acting along the line intersecting both points. This force is proportional to the product of their masses and inversely proportional to the square of the distance between them.

From Kepler to Newton: Kepler’s laws were empirical, based on Tycho Brahe’s meticulous astronomical observations. Kepler described what happened but not why. It was Newton who provided the ‘why’ with his law of universal gravitation.

Newton’s Second Law and Kepler’s Second Law: Newton’s second law (F = ma) can be applied to the motion of planets, showing that the force causing the acceleration (a change in velocity) of a planet in its orbit is the gravitational pull from the Sun. This explains Kepler’s second law, as the planet must move faster when closer to the Sun to sweep out equal areas at equal times due to the conservation of angular momentum.

Newton’s Law of Gravitation and Kepler’s Third Law: Newton’s Law of gravitation can be used to derive Kepler’s third law. It shows that the force keeping a planet in orbit (the centripetal force) is provided by gravity. This force is responsible for the (\(\displaystyle {{T}^{2}}\propto {{a}^{3}}\)) relationship that Kepler observed.

The synthesis of Newton’s and Kepler’s laws allows us to calculate the masses of celestial bodies, understand the orbits of satellites, and even predict the existence of planets around other stars. It’s a cornerstone of classical mechanics and astrophysics.

Application of Kepler’s Laws of Planetary Motion

Kepler’s Laws of Planetary Motion are not just historical scientific achievements; they have practical applications that are crucial in various fields, especially in space exploration and astronomy.

One of the most direct applications of Kepler’s Laws is in planning and executing space missions. Whether it’s sending satellites into orbit or planning interplanetary journeys, understanding the laws of planetary motion is essential.

• Satellite Orbits: By applying Kepler’s Third Law, scientists can calculate the orbital period of a satellite, which helps in determining the altitude at which a satellite must orbit to achieve a desired period, such as geostationary orbit.
• Interplanetary Travel: Spacecraft trajectories are planned using Kepler’s Laws to ensure they take the most efficient path to their destination, conserving fuel and time.

Kepler’s Laws allow astronomers to predict the positions of planets and other celestial bodies with great accuracy.

• Ephemerides: These are tables that provide the positions of naturally occurring astronomical objects in the sky at a given time, and they are created using Kepler’s Laws.
• Celestial Navigation: Mariners and explorers have historically used the positions of celestial bodies for navigation, which relies on the predictable motion described by Kepler’s Laws.

The hunt for planets around other stars, known as exoplanets, also relies on Kepler’s Laws.

• Transit Method: When a planet passes in front of its star, it causes a slight dimming that can be detected and analyzed with Kepler’s Laws to infer the planet’s orbit and size.
• Radial Velocity Method: This method looks for the ‘wobble’ of a star caused by the gravitational pull of an orbiting planet. Kepler’s Laws help in interpreting these observations to find the mass and orbit of the exoplanet.

Kepler’s Laws have broader implications for our understanding of the universe and the laws of physics.

• Gravitational Studies: Kepler’s Laws, combined with Newton’s Law of Universal Gravitation, allow scientists to calculate the masses of celestial bodies.
• Dark Matter Research: By studying the motion of stars within galaxies, astronomers can use Kepler’s Laws to infer the presence of dark matter, which affects the motion of stars and galaxies.

Kepler’s Laws of Planetary Motion are not just theoretical concepts; they are practical tools that scientists and engineers use to explore and understand our universe.

Also Read: Laws of Motion

Solved Examples

Problem 1: Calculate the orbital period of a planet that is 5 AU (astronomical units) away from the Sun. Assume the mass of the Sun is much greater than the mass of the planet.

Solution: Kepler’s Third Law states:

\(\displaystyle T^2 \propto a^3 \)

Where (T) is the orbital period and (a) is the semi-major axis in astronomical units (AU). For planets orbiting the Sun, this relationship simplifies to:

\(\displaystyle T^2 = a^3 \)

Given: (a = 5 AU) , Calculate (T):

\(\displaystyle T^2 = 5^3 \)
\(\displaystyle T^2 = 125 \)
\(\displaystyle T = \sqrt{125}\)
\(\displaystyle T \approx 11.18 \, \text{years} \)

Therefore, the orbital period of the planet is approximately (11.18) years.

Problem 2: A planet orbits the Sun in an elliptical orbit. At its closest approach (perihelion), it is 1 AU from the Sun and has a speed of 30 km/s. Calculate its speed when it is 5 AU from the Sun (aphelion).

Solution: The Law of Conservation of Angular Momentum states that the angular momentum of a planet remains constant if no external torque acts on it. Mathematically:

\(\displaystyle m v_p r_p = m v_a r_a \)

Where (v_p) and (v_a) are the speeds at perihelion and aphelion, respectively, and (r_p) and (r_a) are the distances at perihelion and aphelion, respectively.

Given:

• (\(\displaystyle r_p = 1 \, \text{AU} \))
• (\(\displaystyle v_p = 30 \, \text{km/s} \))
• (\(\displaystyle r_a = 5 \, \text{AU} \))

Calculate (v_a):

\(\displaystyle v_p r_p = v_a r_a \)
\(\displaystyle 30 \times 1 = v_a \times 5 \)
\(\displaystyle v_a = \frac{30}{5} \)
\(\displaystyle v_a = 6 \, \text{km/s} \)

Therefore, the speed of the planet at aphelion is (\(\displaystyle 6 \, \text{km/s} \)).

Problem 3: A planet orbits the Sun in an elliptical orbit with a perihelion distance of 2 AU and an aphelion distance of 8 AU. Calculate the semi-major axis of the orbit.

Solution: The semi-major axis (a) of an elliptical orbit is the average of the perihelion distance (r_p) and aphelion distance (r_a):

\(\displaystyle a = \frac{r_p + r_a}{2} \)

Given:
\(\displaystyle r_p = 2 \, \text{AU} \)
\(\displaystyle r_a = 8 \, \text{AU} \)

Calculate (a):

\(\displaystyle a = \frac{2 + 8}{2} \)
\(\displaystyle a = 5 \, \text{AU} \)

Therefore, the semi-major axis of the planet’s orbit is (\(\displaystyle 5 \, \text{AU} \)).

Problem: Two planets orbit the Sun. Planet A is 1 AU from the Sun, and Planet B is 4 AU from the Sun. Calculate the ratio of their orbital periods.

Solution: Using Kepler’s Third Law:

\(\displaystyle \left(\frac{T_B}{T_A}\right)^2 = \left(\frac{a_B}{a_A}\right)^3 \)

Given:
\(\displaystyle a_A = 1 \, \text{AU} \)
\(\displaystyle a_B = 4 \, \text{AU} \)

Calculate the ratio of the orbital periods:

\(\displaystyle \left(\frac{T_B}{T_A}\right)^2 = \left(\frac{4}{1}\right)^3 \)
\(\displaystyle \left(\frac{T_B}{T_A}\right)^2 = 4^3 \)
\(\displaystyle \left(\frac{T_B}{T_A}\right)^2 = 64 \)
\(\displaystyle \frac{T_B}{T_A} = \sqrt{64} \)
\(\displaystyle \frac{T_B}{T_A} = 8 \)

Therefore, the ratio of the orbital periods (T_B) to (T_A) is (8).

Problem 5: A planet’s orbit has a perihelion distance of 1 AU and an aphelion distance of 5 AU. Calculate the eccentricity of the orbit.

Solution: The eccentricity (e) of an elliptical orbit is given by:

\(\displaystyle e = \frac{r_a – r_p}{r_a + r_p} \)

Given:
\(\displaystyle r_p = 1 \, \text{AU} \)
\(\displaystyle r_a = 5 \, \text{AU} \)

Calculate (e):

\(\displaystyle e = \frac{5 – 1}{5 + 1} \)
\(\displaystyle e = \frac{4}{6} \)
\(\displaystyle e = \frac{2}{3} \)
\(\displaystyle e = 0.67 \)

Therefore, the eccentricity of the planet’s orbit is (0.67).

FAQs