The study of rotational motion, or the motion of objects spinning around an axis, has a rich history that dates back to ancient civilizations. However, the scientific understanding of this type of motion has evolved significantly over time.
The concept of rotation was known to ancient cultures such as the Egyptians, who observed that applying a force to a round object, like a log, would cause it to roll or rotate across the ground. These early observations laid the groundwork for future studies.
Aristotle’s ideas on motion were influential but flawed, as he believed that the natural state of objects was to be at rest. It wasn’t until the Renaissance that Galileo challenged these notions, setting the stage for a better understanding of both linear and rotational motion.
Isaac Newton’s laws of motion, formulated in the 17th century, were pivotal in the study of motion. While Newton himself did not specifically formulate laws for rotational motion, his laws of inertia, force, and action-reaction apply to rotational systems as well.
The real breakthrough in the understanding of rotational motion came with Leonhard Euler in the 18th century. Euler developed the concepts of angular velocity and acceleration, and he introduced the idea of torque, which is the rotational equivalent of force.
The kinematic description of rotational motion, including angular displacement, velocity, and acceleration, was not fully developed until the end of the 19th century by mathematicians like Felix Klein and Arnold Sommerfeld. They, along with others like Joseph-Louis Lagrange and Siméon Denis Poisson, contributed to the foundation of what we now understand as the physics of rotational motion.
In the 20th century, the study of rotational motion expanded with the development of new technologies and the need to understand complex systems, from the spinning of electrons to the orbits of spacecraft.
Angular Velocity
Angular velocity is the rate at which an object rotates or revolves around an axis. It’s denoted by ω and is measured in radians per second (rad/s). Why radians? Because they’re a handy way to talk about angles in terms of the distance around a circle. If an object completes one full rotation (360 degrees or \(\displaystyle 2\pi\) radians) in one second, its angular velocity is \(\displaystyle 2\pi\) rad/s.
Imagine you’re on a merry-go-round. As it spins, you’re moving around a fixed point in the center. Now, angular velocity measures how fast you’re going around that point. It’s like the speedometer in a car, but instead of telling you how fast you’re going in a straight line, it tells you how fast you’re rotating.
\(\displaystyle \omega = \frac{\theta}{t}\)
Where (ω) is the angular velocity, (θ) is the angular displacement (how far you’ve gone around the circle), and (θ) is the time it took.
Angular velocity tells us how quickly an object is changing its position around a circle. For example, if you’re on the edge of the merry-go-round, you’re covering more ground than someone closer to the center, even though you both have the same angular velocity.
Angular Acceleration
Angular acceleration is the rate of change of angular velocity over time, denoted by α. If an object’s angular velocity increases or decreases, it has angular acceleration, measured in radians per second squared (rad/s²).
Think of angular acceleration like the gas pedal for rotation. Just as pressing the pedal makes a car speed up, angular acceleration is what makes an object spin faster or slower. The formula for angular acceleration is:
\(\displaystyle \alpha = \frac{\Delta \omega}{\Delta t} \)
where (∆ω) is the change in angular velocity, and (∆t ) is the change in time.
Example: Imagine you’re on a spinning chair. When you push off the ground with your feet, you start spinning—that’s angular acceleration. If you tuck your legs in, you spin faster, and that’s also due to a change in angular acceleration.
Kinematics of Rotational Motion About a Fixed Axis
Kinematics in rotational motion involves the relationships between angular displacement, angular velocity, and angular acceleration, without considering the forces that cause the motion. Equations similar to linear motion can be used, replacing distance with angle, velocity with angular velocity, and acceleration with angular acceleration.
When we talk about the kinematics of rotational motion, we look at how objects rotate without worrying about what forces cause the rotation. Let’s derive the key equations step by step. First, we need to define our angular quantities:
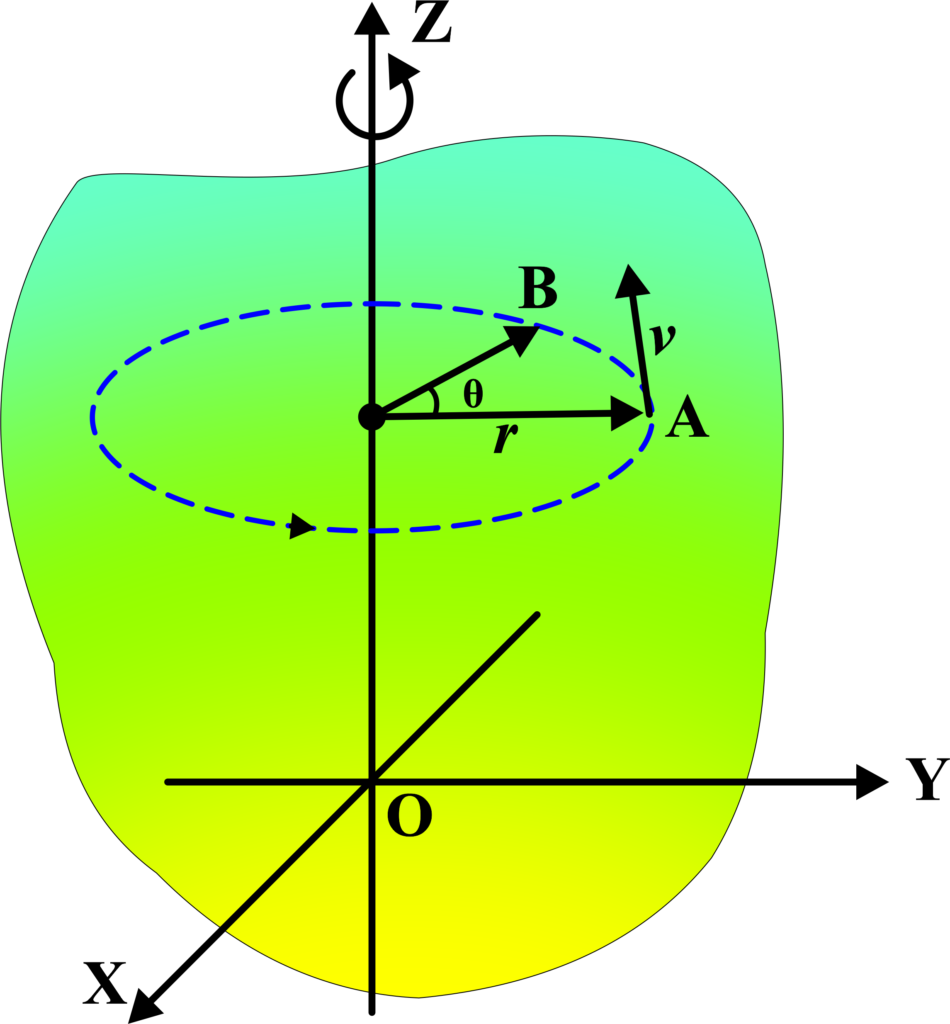
- Angular Displacement (θ): This is the angle through which a point or line has been rotated in a specified sense about a specified axis.
- Angular Velocity (ω): This is how fast the angular displacement is changing. It’s the rate of change of angular displacement.
Angular velocity (ω) is the derivative of angular displacement (θ) with respect to time (t):
\(\displaystyle\omega = \frac{d\theta}{dt}\)
Angular acceleration (α) is the rate at which angular velocity changes with time. It’s the derivative of angular velocity with respect to time:
\(\displaystyle \alpha = \frac{d\omega}{dt}\)
Now, we’ll derive the kinematic equations for rotational motion, analogous to the linear motion equations. If angular acceleration is constant, we can integrate the angular acceleration to find angular velocity:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\omega = \omega_0 + \alpha t }} \end{equation}\)
where (ω0) is the initial angular velocity. To find the angular displacement, we integrate the angular velocity:
\(\displaystyle\begin{equation}\label{eqn:2}\boxed{\boldsymbol{\theta = \theta_0 + \omega_0 t + \frac{1}{2} \alpha t^2 }} \end{equation}\)
where (θ0) is the initial angular displacement. We can also relate the final angular velocity to the initial angular velocity and angular displacement:
\(\displaystyle\begin{equation}\label{eqn:3}\boxed{\boldsymbol{ \omega^2 = \omega_0^2 + 2\alpha(\theta – \theta_0)}} \end{equation}\)
These equations are very similar to linear motion equations, but they apply to rotating objects. They allow us to predict the future state of a rotating object if we know its current state and how its rotation is changing.
These are the basic kinematic equations for rotational motion about a fixed axis. They’re the foundation for understanding how things spin and rotate in physics.
Dynamics of Rotational Motion About a Fixed Axis
When we talk about the dynamics of rotational motion, we’re looking at what causes objects to spin the way they do. It’s like the story behind a spinning top or why planets orbit the way they do. Dynamics refers to the forces and torques that cause an object to rotate. When an object spins around a fixed axis, like a wheel on a car’s axle, it’s experiencing rotational motion about that axis.
Work Done by a Torque
Work in rotational motion is done by a torque. Torque is the rotational equivalent of force and causes changes in rotational motion. The work done by a torque is the product of the torque and the angular displacement.
Torque (τ) is like a twist or a force that causes an object to rotate. The amount of torque depends on how far from the axis the force is applied and the magnitude of the force itself.
The work (W) done by torque is the product of the torque and the angular displacement (θ) it produces:
\(\displaystyle W = \tau \theta \)
But remember, the angle must be in radians, and the torque must be the component of the force that causes the rotation. Torque is the product of the force (F) and the lever arm (r), which is the perpendicular distance from the axis of rotation to the point where the force is applied.
\(\displaystyle \tau = rF \)
Work is done when a force causes displacement. In rotational motion, this displacement is an angle (θ).
\(\displaystyle W = F \cdot (r\theta) \)
Since (τ= rF), we can substitute to get the work done by a torque.
\(\displaystyle\begin{equation}\label{eqn:4}\boxed{\boldsymbol{W = \tau \theta }} \end{equation}\)
This equation tells us that the work done by a torque is directly proportional to both the torque and the angle through which it rotates the object.
Imagine you’re using a wrench to loosen a bolt. You apply a force at the end of the wrench, and the bolt turns. The work you’ve done is the torque (from the force and the length of the wrench) times the angle you’ve turned the bolt.
The work done by a torque in rotational motion is similar to the work done by a force in linear motion. It’s all about the energy transferred by the torque to cause rotation.
Also Read: Torque And Angular Momentum
Kinetic energy
Kinetic energy is the energy of motion. For rotational motion, the kinetic energy is due to the object spinning around an axis. Let’s break down how we can derive an expression for this type of kinetic energy.
A rigid body rotating about a fixed axis can be thought of as a collection of particles, each moving in a circular path around the axis. Each particle has kinetic energy due to its motion. For a particle with mass (m) moving at a velocity (v), the kinetic energy (KE) is:
\(\displaystyle KE = \frac{1}{2}mv^2 \)
The linear velocity (v) of a particle at a distance (r) from the axis of rotation is related to the angular velocity (ω) by:
\(\displaystyle v = \omega r \)
Substituting (v) into the kinetic energy expression and summing up the kinetic energies of all particles, we get the total kinetic energy (KEtotal):
\(\displaystyle KE_{total} = \sum \frac{1}{2}m(\omega r)^2 \)
The moment of inertia (I) is the sum of the products of the mass of each particle and the square of its distance from the axis:
\(\displaystyle I = \sum mr^2 \)
Now, we combine the expressions for kinetic energy and moment of inertia:
\(\displaystyle KE_{total} = \frac{1}{2}\omega^2 \sum mr^2 \)
Since (I = ∑ mr2), we can write the total kinetic energy as:
\(\displaystyle\begin{equation}\label{eqn:5}\boxed{\boldsymbol{KE_{total} = \frac{1}{2}I\omega^2 }} \end{equation}\)
This is the expression for the kinetic energy of a body rotating about a fixed axis. It shows that the rotational kinetic energy depends on the moment of inertia and the square of the angular velocity.
Just like how the kinetic energy of an object moving in a straight line depends on its mass and the square of its velocity, the rotational kinetic energy depends on the distribution of the object’s mass around the axis (moment of inertia) and how fast it’s spinning (angular velocity).
Power
Power is the rate at which work is done. In rotational motion, it’s the rate at which torque does work on an object to cause it to rotate.
We know that the work done by a torque (τ) over some angular displacement (θ) is:
\(\displaystyle W = \tau \theta \)
Power (P) is the rate at which work is done, so it’s the work done per unit time (t):
\(\displaystyle P = \frac{W}{t} \)
If the angular displacement occurs over a small time interval, we can express work as:
\(\displaystyle W = \tau \Delta \theta \)
where (∆θ) is the change in angular position.
Since angular velocity (ω) is the rate of change of angular displacement, we have:
\(\displaystyle \omega = \frac{\Delta \theta}{\Delta t} \)
Rearranging this, we get:
\(\displaystyle \Delta \theta = \omega \Delta t \)
Substituting this into the expression for work, we get:
\(\displaystyle W = \tau \omega \Delta t \)
Now, substituting this into the power equation, we get:
\(\displaystyle P = \frac{\tau \omega \Delta t}{\Delta t} \)
The (∆t) terms cancel out, leaving us with the expression for power in rotational motion:
\(\displaystyle\begin{equation}\label{eqn:6}\boxed{\boldsymbol{P = \tau \omega }} \end{equation}\)
This tells us that the power in rotational motion is the product of the torque and the angular velocity. It’s the rotational equivalent of the linear power expression (P = Fv), where (F) is force and (v) is velocity.
The power in rotational motion is how fast the torque is doing work to spin an object. It’s a measure of the “oomph” behind the rotation, telling us how quickly energy is being transferred to cause the rotation.
Angular Momentum
Angular momentum is a measure of the amount of rotation an object has, taking into account its mass distribution and speed of rotation. It’s the rotational equivalent of linear momentum.
A rigid body rotating about a fixed axis can be thought of as a collection of particles, each contributing to the body’s angular momentum. For a single particle with mass (m) moving in a circle with radius (r) and linear velocity (v), the angular momentum (L) is defined as:
\(\displaystyle L = r \times p \)
where (p) is the linear momentum (mv) of the particle, and ( r × p ) represents the cross product of the radius vector and the linear momentum vector.
The linear velocity (v) of a particle at a distance (r) from the axis of rotation is related to the angular velocity (ω) by:
\(\displaystyle v = \omega r \)
Substituting the expression for (v) into the angular momentum definition, we get:
\(\displaystyle L = r \times (m \omega r)\)
Since (r × r) is zero (because the cross product of any vector with itself is zero), we simplify the expression to:
\(\displaystyle L = m r^2 \omega \)
The total angular momentum (Ltotal) of the rigid body is the sum of the angular momenta of all its particles:
\(\displaystyle L_{total} = \sum m_i r_i^2 \omega \)
The moment of inertia (I) of the rigid body is the sum of the products of the mass of each particle and the square of its distance from the axis:
\(\displaystyle I = \sum m_i r_i^2 \)
Combining the expressions for (I) and (Ltotal), we get the final expression for the angular momentum of a body rotating about a fixed axis:
\(\displaystyle\begin{equation}\label{eqn:7}\boxed{\boldsymbol{L_{total} = I \omega }} \end{equation}\)
This is the expression for the angular momentum of a body rotating about a fixed axis. It shows that the angular momentum depends on the distribution of the body’s mass and how fast it’s spinning.
Angular momentum is conserved in a closed system unless acted upon by an external torque. This principle is used in various applications, from understanding how ice skaters spin to the orbits of celestial bodies.
Conservation of Angular Momentum
The principle of conservation of angular momentum states that if no external torque acts on a system, the total angular momentum remains constant. This principle explains why a figure skater spins faster when they pull their arms in—they are reducing their moment of inertia, which increases their angular velocity to conserve angular momentum.
Imagine you’re an ice skater spinning with your arms outstretched. When you pull your arms in, you spin faster. This happens because of the conservation of angular momentum.
Angular momentum is like the ‘spin’ version of momentum. It’s a measure of how much rotation an object has and depends on two things:
- The distribution of mass around the axis (moment of inertia, (I)
- How fast it’s spinning (angular velocity, (\omega)
The angular momentum (L) of an object is given by the product of its moment of inertia and its angular velocity:
\(\displaystyle L = I \omega \)
The principle of conservation of angular momentum tells us that if no external force or torque is messing with the spin, the angular momentum will stay the same. It’s a constant value, like the amount of money in a locked savings account.
When our ice skater pulls their arms in, they’re reducing their moment of inertia (I). Since angular momentum (L) must stay the same, and (I) is getting smaller, the angular velocity (ω) must increase to balance it out. That’s why the skater spins faster.
If the initial angular momentum is (Li) and the final angular momentum is (Lf), and there are no external torques, then:
\(\displaystyle L_i = L_f \)
In other words:
\(\displaystyle I_i \omega_i = I_f \omega_f \)
where (Ii) and (ωi) are the initial moment of inertia and angular velocity, and (If) and (ωf) are the final values.
This principle isn’t just for ice skaters. It’s crucial for understanding how planets orbit, how engines work, and even how galaxies hold together. It’s a fundamental rule of the universe that keeps things spinning.
Comparison of Translational and Rotational Motion
| Aspect | Translational Motion | Rotational Motion | Formula |
|---|---|---|---|
| Definition | Motion in which all parts of an object move in the same direction and through the same distance. | Motion in which an object turns about an internal axis. | N/A |
| Path | Straight or curved line. | Circular path around a fixed axis. | N/A |
| Displacement | Linear displacement from one point to another. | Angular displacement around the axis of rotation. | Linear: (s) Angular: (θ) |
| Velocity | The force causes linear acceleration. | Angular velocity is the rate of change of angular displacement. | Linear: \(\displaystyle v = \frac{ds}{dt} \) Angular: \(\displaystyle \omega = \frac{d\theta}{dt} \) |
| Acceleration | Linear acceleration is the rate of change of linear velocity. | Angular acceleration is the rate of change of angular velocity. | Linear: \(\displaystyle a = \frac{dv}{dt} \) Angular: \(\displaystyle \alpha = \frac{d\omega}{dt} \) |
| Inertia | Mass, which resists changes in linear motion. | Moment of inertia, which resists changes in rotational motion. | Linear: (m) Angular: (I) |
| Force | Force causes linear acceleration. | Torque causes angular acceleration. | Linear: ( F = ma ) Angular: \(\displaystyle \tau = I\alpha \) |
| Equations of Motion | Equations involve distance, speed, time, and linear acceleration. | Equations involve angle, angular velocity, angular acceleration, and time. | Linear: \(\displaystyle s = ut + \frac{1}{2}at^2\) Angular: \(\displaystyle \theta = \omega t + \frac{1}{2}\alpha t^2 \) |
| Energy | Kinetic energy is the energy of motion. | Rotational kinetic energy is the energy of rotational motion. | Linear: \(\displaystyle KE = \frac{1}{2}mv^2 \) Angular: \(\displaystyle KE_{rot} = \frac{1}{2}I\omega^2 \) |
| Momentum | Linear momentum is the product of mass and linear velocity. | Angular momentum is the product of moment of inertia and angular velocity. | Linear: (p = mv) Angular: \(\displaystyle L = I\omega \) |
| Conservation Laws | Conservation of linear momentum. | Conservation of angular momentum. | Linear: (pinitial = pfinal) Angular: (Linitial= Lfinal) |
Solved Examples
Example 1: A wheel initially at rest accelerates uniformly at \(\displaystyle 5 \, \text{rad/s}^2 \) for (4). Calculate its angular velocity at the end of this time interval.
Solution: We can use the formula for angular velocity (ω) in uniformly accelerated rotational motion:
\(\displaystyle \omega = \omega_0 + \alpha t \)
Given \(\displaystyle \omega_0 = 0 \, \text{rad/s} \), \(\displaystyle \alpha = 5 \, \text{rad/s}^2 \), and (t = 4 s), substituting these values:
\(\displaystyle \omega = 0 + 5 \times 4 = 20 \, \text{rad/s} \)
Therefore, the angular velocity of the wheel at the end of (4s) is (20 rad/s).
Example 2: A disk rotates with an angular velocity of (4 rad/s) and comes to a stop after (10 s) due to a constant angular deceleration. Calculate its angular acceleration.
Solution: We can use the formula for angular acceleration (α) in uniformly decelerated rotational motion:
\(\displaystyle \alpha = -\frac{\omega}{t} \)
Given \(\displaystyle \omega = 0 \, \text{rad/s} \) (as the disk comes to a stop) and (t = 10 s), substituting these values:
\(\displaystyle \alpha = -\frac{0}{10} = 0 \, \text{rad/s}^2 \)
Therefore, the angular acceleration of the disk is (0 rad/s2 ).
Example 3: A flywheel undergoes uniform angular acceleration from rest to (10 rad/s) in (5 s). Calculate the total angular displacement during this time interval.
Solution: We can use the formula for angular displacement (θ) in uniformly accelerated rotational motion:
\(\displaystyle \theta = \omega_0 t + \frac{1}{2} \alpha t^2 \)
Given \(\displaystyle \omega_0 = 0 \, \text{rad/s} \), \(\displaystyle \omega = 10 \, \text{rad/s} \), and (t = 5 s), we need to find (α) first:
\(\displaystyle \alpha = \frac{\omega – \omega_0}{t} = \frac{10 – 0}{5} = 2 \, \text{rad/s}^2 \)
Now, substituting (α) into the formula for angular displacement:
\(\displaystyle \theta = 0 \times 5 + \frac{1}{2} \times 2 \times 5^2 = 0 + 25 = 25 \, \text{rad} \)
Therefore, the total angular displacement during (5 s) is (25 rad).
Example 4: A fan blade rotates with an angular velocity of (8 rad/s) and decelerates uniformly until it comes to a stop after (4 s). Calculate its angular deceleration.
Solution: We can use the formula for angular acceleration (α) in uniformly decelerated rotational motion:
\(\displaystyle \alpha = -\frac{\omega}{t} \)
Given \(\displaystyle\omega = 0 \, \text{rad/s} \) and (t = 4 s} ), substituting these values:
\(\displaystyle \alpha = -\frac{0}{4} = 0 \, \text{rad/s}^2 \)
Therefore, the angular deceleration of the fan blade is (0 rad/s2 ).
Example 5: A wheel initially rotates with an angular velocity of (10 rad/s) and undergoes constant angular deceleration until it comes to a stop after (6 s). Calculate its angular velocity at the end of this time interval.
Solution: We can use the formula for angular velocity (ω) in uniformly decelerated rotational motion:
\(\displaystyle \omega = \omega_0 + \alpha t \)
Given \(\displaystyle \omega_0 = 10 \, \text{rad/s} \), (α) is negative as it represents deceleration, and (t = 6 s), we need to find (α) first:
\(\displaystyle \alpha = -\frac{\omega – \omega_0}{t} = -\frac{0 – 10}{6} = \frac{5}{3} \, \text{rad/s}^2 \)
Now, substituting (α) into the formula for angular velocity:
\(\displaystyle \omega = 10 + \frac{5}{3} \times 6 = 10 + 10 = 20 \, \text{rad/s} \)
Therefore, the angular velocity of the wheel at the end of (6 s) is (20 rad/s} ).
FAQs
What is meant by rotational motion around a fixed axis in physics?
Rotational motion around a fixed axis refers to the motion of an object as it rotates about an axis that remains fixed in space. This type of motion is commonly observed in objects like spinning tops, wheels, and planets orbiting the Sun.
How is angular displacement defined in the kinematics of rotational motion?
Angular displacement is a measure of the change in orientation of an object undergoing rotational motion around a fixed axis. It is the angle through which the object has rotated and is usually measured in radians.
Can you explain the concept of angular velocity in rotational motion?
Angular velocity is the rate of change of angular displacement with respect to time. It represents how quickly an object is rotating around a fixed axis and is typically measured in radians per second (rad/s).
What is torque, and how does it relate to the dynamics of rotational motion?
Torque is a measure of the rotational force applied to an object, causing it to rotate around a fixed axis. In the dynamics of rotational motion, torque is responsible for producing angular acceleration, similar to how force produces linear acceleration in translational motion.
How is angular acceleration defined in rotational dynamics?
Angular acceleration is the rate of change of angular velocity with respect to time. It represents how quickly the angular velocity of an object undergoing rotational motion changes, either increasing or decreasing, and is typically measured in radians per second squared (rad/s²).
Can you explain the relationship between torque, moment of inertia, and angular acceleration?
According to Newton’s second law for rotational motion, the torque acting on an object is equal to the product of its moment of inertia and its angular acceleration. Mathematically, this relationship is expressed as (τ = I α ).
What are some real-world examples demonstrating the kinematics and dynamics of rotational motion around a fixed axis?
Examples include the spinning of a wheel on a car, the rotation of a wind turbine blade, and the movement of a gyroscope. In each case, the object undergoes rotational motion around a fixed axis, with its kinematics and dynamics governed by principles such as angular displacement, angular velocity, torque, and angular acceleration.
