The journey of the Second Law of Thermodynamics began in the early 19th century with the work of French engineer Sadi Carnot. He was curious about improving the efficiency of steam engines, which were vital during the Industrial Revolution. In 1824, Carnot made a groundbreaking discovery: he found an upper limit to the efficiency of converting heat to work in a heat engine. This was the first time someone had put a theoretical limit on the power of machines, and it laid the groundwork for the Second Law.
As the century progressed, two other scientists, Rudolf Clausius from Germany and Lord Kelvin from the UK, expanded on Carnot’s ideas. They observed that heat doesn’t just flow randomly; it always moves from hotter objects to cooler ones. This might seem obvious to us now, but back then, it was a revelation that changed how people thought about energy and work.
Clausius introduced the term “entropy” in the 1850s to describe this natural tendency of systems to become more disordered over time. He also gave us one of the most famous statements of the Second Law: “Heat can never pass from a colder to a warmer body without some other change, connected in addition to that, occurring at the same time.”
These ideas were purely observation-based and didn’t have a solid theoretical foundation yet. It wasn’t until the end of the 19th century, with the rise of statistical mechanics, that scientists could explain the Second Law on a microscopic level, using the behavior of atoms and molecules.
The Second Law started as an empirical observation, became a fundamental law of thermodynamics, and was eventually explained through the lens of probability and statistics. It’s a beautiful example of how scientific understanding evolves, from practical problems like making better engines to deep insights into the nature of the universe itself.
What is the Second Law of Thermodynamics?
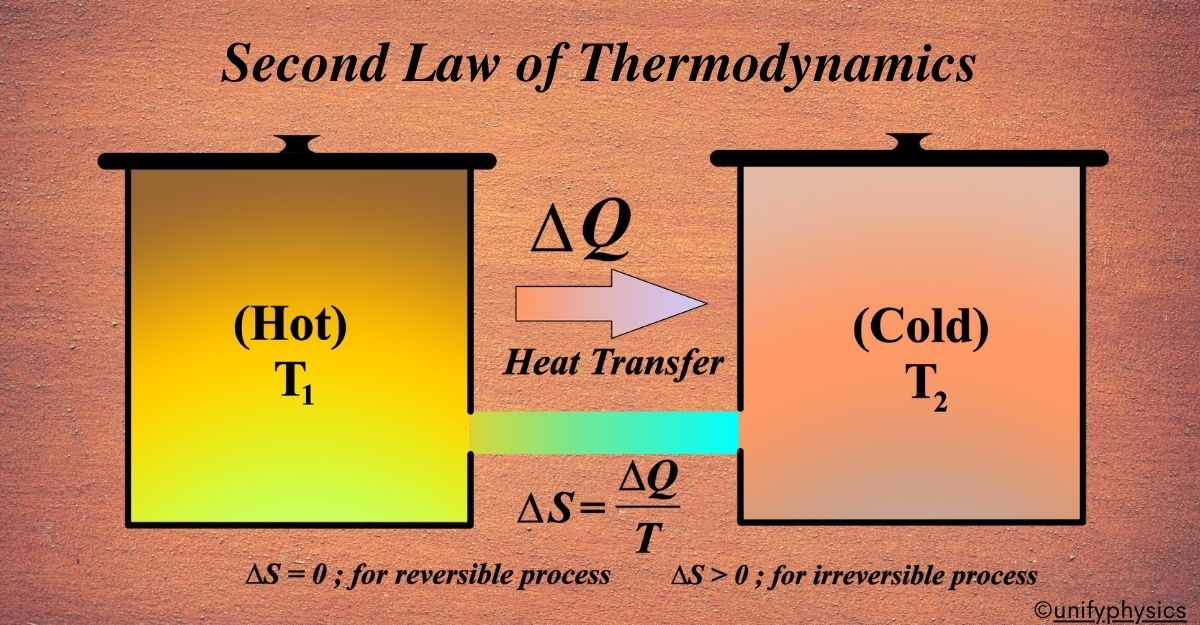
The Second Law states that the total entropy, or disorder, of an isolated system can never decrease over time. It means that systems naturally progress towards a state of maximum entropy or disorder.
Imagine you have a room with two sections, one hot and one cold. If you remove the barrier between them, the heat will naturally flow from the hot side to the cold side until both sides reach the same temperature. This is a bit like how the Second Law of Thermodynamics works.
In technical terms, the Second Law tells us that in any natural process, the total entropy of an isolated system will always increase over time. Entropy is a scientific way of talking about how disordered things are. So, the Second Law is saying that things tend to get more mixed up and less orderly as time goes on.
Here’s a simpler way to think about it: If you have a neat bedroom, it doesn’t stay that way on its own. Over time, it gets messier unless you put in some effort to clean it up. In the universe, things naturally go from being orderly (like a tidy room) to being disorderly (like a messy room), and it takes extra energy to maintain or increase order.
This law is super important because it explains why certain things happen the way they do, like why we can’t build a perpetual motion machine—a machine that would run forever without any extra energy. It also tells us why we need to put in work to get work out, like needing fuel to run a car engine.
Entropy
Entropy is a measure of the randomness or disorder within a system. The more ways a system can be arranged without changing its external properties, the higher its entropy.
Entropy is a bit like the level of messiness in your room. If everything is neatly organized and in its place, your room has low entropy. But if your clothes are all over the floor and books are scattered on your desk, the entropy is high because there’s a lot of disorder.
In physics, entropy is a measure of this disorder or randomness in a system. It’s represented by the letter S and is usually measured in units called joules per kelvin (J/K). The more ways the parts of a system can be arranged without changing the overall system, the higher the entropy.
In a more scientific sense, entropy measures the number of different ways we can arrange the particles in a system without changing their overall appearance. For example, if we have a gas in a box, there are lots of ways the gas particles can move around and still look like the same gas to us. Each of these arrangements is called a ‘microstate,’ and the more microstates there are, the higher the entropy.
Now, the Second Law of Thermodynamics tells us that in any natural process, entropy tends to increase. This means that things naturally go from being orderly to being disorderly. Like our room example, without putting in effort to clean it, the room will generally get messier over time. This is why heat flows from hot to cold and why we can’t get energy for free; there’s always some energy that becomes disordered and can’t be used to do work.
Microstate
Imagine you’re playing a video game where you can customize your character’s appearance. Each combination of clothes, hair, and accessories is one specific way your character can look. In physics, each specific arrangement of particles in a system is called a ‘microstate.’
A microstate is a detailed description of a system at a microscopic level. It tells us exactly where each particle is and how fast it’s moving at a particular moment. Just like there are many ways to customize your character in the game, there are countless microstates for particles in a system.
For example, think about a gas in a box. If we could see all the tiny gas molecules, each one would have a specific position and speed. Every possible snapshot of where all those molecules are and how they’re moving is a different microstate.
The Second Law of Thermodynamics is interested in microstates because it’s all about probability. Systems change over time, and they tend to move toward the microstate that’s most likely, which usually means the one with the highest entropy or the most disorder. The more microstates there are, the higher the entropy, and the more likely the system is to be found in one of those microstates.
Also Read: Zeroth Law of Thermodynamics
Different Statements of the Second Law of Thermodynamics
Kelvin-Planck Statement
“The Kelvin-Planck Statement of the Second Law of Thermodynamics says that it’s impossible to build a machine that can take heat from one place and turn it entirely into work without leaving some of the heat behind.”
Imagine you have a steam engine that runs by boiling water to create steam, which then pushes on pistons to do work, like moving a train. According to the Kelvin-Planck statement, this steam engine can’t convert all the heat from the boiling water into the work of moving the train. Some of that heat will always be lost to the surroundings or has to be transferred to a cooler place, like a condenser where the steam turns back into the water.
This is because if an engine could convert all the heat into work without losing any heat, it would be a ‘perpetual motion machine of the second kind,’ which is a machine that could run forever without adding more energy. But the Second Law tells us that this kind of machine is impossible because there’s always some waste heat that can’t be turned into work.
In real life, all heat engines, whether they’re in cars, power plants, or trains, have to release some heat into the environment. They can’t be 100% efficient because of the Kelvin-Planck statement of the Second Law of Thermodynamics. This is why engineers are always looking for ways to make engines more efficient, but they know they can’t reach perfect efficiency.
The Kelvin-Planck statement helps us understand the limits of energy conversion and why perpetual motion machines (machines that would run forever without any energy input) are impossible according to the laws of physics.
Clausius Statement
“The Clausius Statement of the Second Law of Thermodynamics tells us that heat won’t naturally flow from a colder object to a hotter one without some outside help, like using energy or a special device.”
OR
The Clausius Statement is about refrigerators and heat pumps—devices that move heat from a cooler place to a warmer place. It says that you can’t transfer heat from a cold object to a hot object without adding work or energy into the system.
Think about your refrigerator at home. It keeps your food cold by moving heat from the inside of the fridge (which is cool) to the outside (which is warmer). According to the Clausius Statement, this can’t happen by itself; the fridge needs an external power source, like electricity, to do this work.
The Clausius Statement tells us that heat naturally flows from hot to cold, not the other way around. If we want to make it go from cold to hot, we need to use a heat pump or a refrigerator, and we need to put in energy to make it work.
This is why, for example, when you touch a cold soda can, it doesn’t spontaneously get colder and make your hand hotter. Instead, your hand warms the can because heat flows from your warmer hand to the colder can.
So, the Clausius Statement helps us understand the direction of natural heat flow and the work needed to reverse that flow. It’s a fundamental principle that explains why we can’t create a perpetual motion machine of the second kind—a machine that would continuously transfer heat from cold to hot without needing any energy input.
Equivalence of Clausius and Kelvin-Planck Statements
The Clausius and Kelvin-Planck statements might seem different at first glance because they talk about different things. The Kelvin-Planck statement is about heat engines, which convert heat into work, and says you can’t just take heat from a hot source and turn it all into work without losing some heat. The Clausius statement is about refrigerators and heat pumps, which move heat from cold to hot, and says you can’t do that without putting in work.
But here’s the thing: these two statements are saying the same fundamental truth in different ways. They both tell us that you can’t get something for nothing when it comes to heat and work.
Imagine you have a heat engine (like a steam engine) that’s trying to break the Kelvin-Planck statement by turning all its heat into work without losing any heat. Now, if you also have a refrigerator trying to break the Clausius statement by moving heat from a cold place to a hot place without work, you could combine these two machines. The heat engine would power the refrigerator, and the refrigerator would move heat back to the heat engine’s hot source.
If this were possible, you’d have a perpetual motion machine, because the heat engine would keep running forever without any new energy. But we know that’s impossible because of the Second Law of Thermodynamics. So, if one statement were false, the other would be too, because you’d be able to create a machine that breaks the fundamental rules of thermodynamics.
In summary, the equivalence of the Clausius and Kelvin-Planck statements means that if you could break one of these rules, you could break the other, and that would mean you could make a perpetual motion machine. Since we know that’s not possible, both statements must be true, and they’re just two sides of the same coin in the world of thermodynamics.
Perpetual Motion Machine of the Second Kind
Imagine you have a magical water bottle that never runs out of water. You drink from it, and somehow, it refills itself instantly without any help. This is similar to what a Perpetual Motion Machine of the Second Kind claims to do but with energy.
A Perpetual Motion Machine of the Second Kind is a hypothetical device that could continuously convert heat into work without needing any external energy and without any heat loss. It would be like having an engine that runs forever on the heat from its surroundings without ever stopping or needing fuel.
However, this kind of machine is impossible according to the laws of physics, specifically the Second Law of Thermodynamics. This law tells us that some energy is always lost as heat when converting it into work. In other words, you can’t get more out of a system than you put into it.
So, a Perpetual Motion Machine of the Second Kind would violate this fundamental law by creating work without losing any heat, which goes against everything we know about how energy works. It’s like trying to win a game where the rules say you can’t score points – it just can’t be done.
Second Law of Thermodynamics Equation
The equation for the Second Law of Thermodynamics is a simple but powerful one:
\(\displaystyle\begin{equation}\label{eqn:1}\boxed{\boldsymbol{\Delta S_{univ} > 0 }} \end{equation}\)
where \(\displaystyle\Delta S_{univ} \) is the change in the entropy of the universe.
Let’s use an example to make this clearer. Imagine you have a block of ice (which is quite orderly) and it melts into water (which is less orderly). The entropy of the water is higher than that of the ice because the molecules are more randomly arranged when they’re liquid than when they’re solid.
This equation tells us that whenever something happens on its own—like ice melting, a room getting messy, or even mixing cream into coffee—the total entropy, or disorder, of the universe increases. It’s a fundamental rule that helps us predict whether a process can occur spontaneously.
Derivation
Consider an isolated system, which means no matter or energy is exchanged with the surroundings. The system plus its surroundings can be considered as the universe in thermodynamic terms. The change in entropy (∆S) of a system during a process is defined by the heat transferred (Q) divided by the temperature (T) at which the transfer occurs, assuming the process is reversible. So, \(\displaystyle\Delta S = \frac{Q}{T} \).
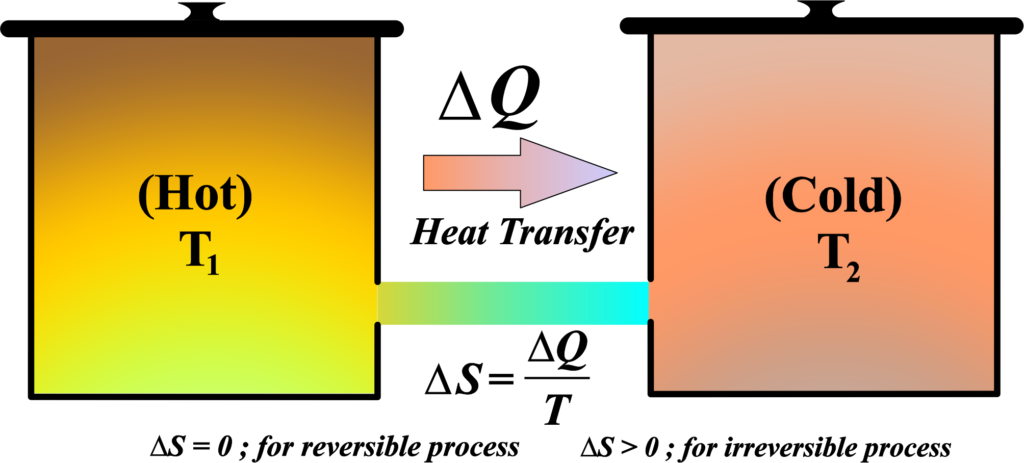
In a reversible process, the system is in equilibrium, and the entropy change of the system and surroundings is zero. However, in a real, irreversible process, the entropy of the system and its surroundings increases.
Since the universe is an isolated system, we can say that the total entropy change of the universe (\(\displaystyle\Delta S_{univ} \)) is the sum of the entropy change of the system (\(\displaystyle\Delta S_{sys} \)) and the entropy change of the surroundings (\(\displaystyle \Delta S_{surr} \)). So, for a system and its surroundings, the entropy changes are:
\(\displaystyle\Delta S_{system} = \frac{Q_{system}}{T}\)
\(\displaystyle\Delta S_{surroundings} = \frac{Q_{surroundings}}{T}\)
The total change in entropy, which is the sum of the changes in both the system and its surroundings, represents the entropy change of the universe:
\(\displaystyle\Delta S_{universe} = \Delta S_{system} + \Delta S_{surroundings}\)
Reversible Process: In a perfect world, where processes are reversible and everything happens without any loss, the heat lost by the system is the same as the heat gained by the surroundings. This means:
\(\displaystyle Q_{system} = -Q_{surroundings}\)
And because of this perfect balance, the total entropy change of the universe would be zero:
\(\displaystyle\Delta S_{universe} = 0\)
Irreversible Process: But in the real world, processes are not perfect; they’re irreversible. For example, if an ideal gas expands and absorbs heat, the heat absorbed (Q) can be represented by the equation:
\(\displaystyle Q_{irreversible} = nRT \ln \left(\frac{V_2}{V_1}\right)\)
Here, (V1) is the initial volume, (V2) is the final volume, (T) is the temperature, (R) is the universal gas constant, and (n) is the number of moles of the gas. The entropy change for the universe in an irreversible process is then:
\(\displaystyle\Delta S_{universe} = \frac{Q_{irreversible}}{T} = nR \ln \left(\frac{V_2}{V_1}\right)\)
Since (V2) is greater than (V1) (the gas expands), the entropy change of the universe is greater than zero:
\(\displaystyle\Delta S_{universe} > 0\)
Combining both reversible and irreversible processes, we can say that the entropy change of the universe is always zero or positive:
\(\displaystyle\Delta S_{universe} \geq 0\)
This means that for a perfectly balanced, reversible process, the entropy change is zero, but for all real-life, irreversible processes, entropy increases. This could be due to work done on the system, which might cause friction or viscosity, or because of a chemical reaction. This mathematical formulation shows that the Second Law of Thermodynamics is a statement about the direction of natural processes, indicating that the total entropy of the universe increases for any spontaneous process.
Application
This law helps us understand why not all heat can be converted into work in engines and why refrigerators require external energy to operate. The Second Law of Thermodynamics has several practical applications in our daily lives and various technologies. Here are some key examples:
- Heat Engines: This law is fundamental to the operation of heat engines, like the ones found in cars and power plants. It explains why engines need a cold space (like the environment) to dump their waste heat and can’t convert 100% of their heat energy into work.
- Refrigerators and Air Conditioners: These devices move heat from a cooler area (inside the fridge or a room) to a warmer area (outside). The Second Law tells us that to do this, they need an external energy source, like electricity, because heat doesn’t naturally flow from cold to hot.
- In living organisms, the Second Law explains why we need to consume food to maintain order within our bodies. Without a constant input of energy, our bodies would become more disordered, leading to death.
- The Second Law also applies to the field of information technology. It’s related to the concept of entropy in data transmission, where increasing disorder can lead to loss of information, requiring error correction methods.
- On a universal scale, the Second Law predicts the eventual ‘heat death’ of the universe, where all energy is evenly distributed, and no more work can be extracted from thermal differences.
- In chemical manufacturing, the Second Law helps engineers understand and design processes that are more energy-efficient and sustainable.
- The law sets the ultimate efficiency limit for all energy conversion processes, prompting the development of better technologies to get as close to this limit as possible.
Limitations
The Second Law does not specify how fast processes occur and assumes that systems are closed and isolated from external influences. The Second Law of Thermodynamics is a fundamental principle that has broad implications in physics and engineering. However, like all scientific laws, it has its limitations:
- The Second Law deals with the natural tendency of processes to be irreversible. For example, once you mix cream into coffee, you can’t separate them back into cream and coffee easily. This law doesn’t explain how to reverse such processes.
- It primarily applies to closed systems, where no matter or energy is exchanged with the surroundings. In real-world applications, perfectly closed systems are rare, and most systems are open to some extent.
- The Second Law doesn’t specify the rate at which processes occur. It tells us that entropy will increase over time, but it doesn’t say how quickly this will happen.
- While the Second Law predicts the overall direction of processes, it doesn’t give us detailed information about the microscopic state of each particle within a system.
- The law sets limits on the efficiency of energy conversion processes but doesn’t provide a method to achieve maximum efficiency within those limits.
- There’s a misconception that the Second Law only applies to closed systems. However, its principles can be observed in a wide range of scenarios, including open and isolated systems.
FAQs
Q: What is the Second Law of Thermodynamics, and why is it often associated with the concept of entropy?
- Answer: The Second Law of Thermodynamics states that the entropy of an isolated system tends to increase over time, leading to a decrease in the system’s ability to do work. Entropy is a measure of the disorder or randomness of a system, and the Second Law emphasizes the tendency of natural processes to move towards states of higher entropy, reflecting the natural progression towards increased disorder.
Q: Can you explain why perpetual motion machines are impossible according to the Second Law of Thermodynamics?
- Answer: Perpetual motion machines, which produce work indefinitely without any external energy input, violate the Second Law of Thermodynamics. This is because such machines would operate in a manner that decreases the entropy of the system, which is contrary to the natural tendency of entropy to increase over time. Thus, the Second Law dictates that perpetual motion machines are impossible.
Q: How does the Second Law of Thermodynamics relate to the concept of heat engines and their efficiency?
- Answer: The Second Law of Thermodynamics places limits on the efficiency of heat engines by stating that no engine can convert all of the input heat into useful work. This is because some heat must always be rejected by the surroundings, increasing the entropy of the system. The maximum possible efficiency of a heat engine is determined by the Carnot efficiency, which is based on the temperatures of the hot and cold reservoirs.
Q: What role does the concept of reversibility play in understanding the Second Law of Thermodynamics?
- Answer: The concept of reversibility refers to the ability of a process to be reversed without any net change in entropy. According to the Second Law, reversible processes are idealized and represent the maximum theoretical efficiency of a process. However, real-world processes are often irreversible, leading to increases in entropy and decrease in available energy.
Q: Can you provide examples of everyday processes that illustrate the Second Law of Thermodynamics?
- Answer: Everyday processes such as mixing cream into coffee, the cooling of hot tea in a room, and the rusting of metal all exemplify the Second Law of Thermodynamics. These processes result in increased disorder (entropy) over time, demonstrating the natural tendency of systems to move towards states of higher entropy.
Q: How does the Second Law of Thermodynamics apply to the concept of heat transfer?
- Answer: The Second Law of Thermodynamics dictates the direction of heat transfer, stating that heat flows spontaneously from regions of higher temperature to regions of lower temperature. This principle underlies various heat transfer processes, such as conduction, convection, and radiation, and helps explain the irreversibility of these processes.
Q: Can the Second Law of Thermodynamics be violated under certain conditions?
- Answer: No, the Second Law of Thermodynamics is a fundamental principle of physics and cannot be violated. It applies universally to all natural processes and is upheld under a wide range of conditions. Any apparent violations would indicate errors in measurement or misunderstanding of the underlying thermodynamic principles.